Cette réponse n'est rien de plus qu'une variante de la réponse de Sklivv. Je souhaite simplement discuter de quelques idées quantitatives issues de la réponse de Sklivv et discuter de ce que je comprends (d'un ami ingénieur aérospatial) comme étant une erreur conceptuelle courante - que l'application de "simples effets de surface" et de "l'application du principe de Bernoulli" est erronée. Ces "simples effets de surface et le principe de Bernoulli" découlent de l'idée de Sklivv, comme j'espère le préciser. Tout dans la physique des avions commence et se termine par "les avions poussent l'air vers le bas, de sorte que l'air pousse les avions vers le haut" . Cette réponse est écrite pour être compréhensible par quelqu'un comme moi qui ne sait rien de la dynamique des fluides - à part:
-
Les problèmes 2D mathématiquement élégants et très agréables abordés avec la théorie des variables complexes (voir Trouver des points de stagnation à partir du potentiel complexe);
-
Que je sais qu'il y a un prix Clay Mathematics à gagner pour quiconque peut prouver l'existence de, ou donner un contre-exemple contre, l'existence de solutions lisses et globalement bien définies aux équations de Navier-Stokes;
-
Que mes collègues et amis ingénieurs aérospatiaux me disent que la preuve expérimentale est toujours reine dans ce domaine : la plupart des dynamiques réelles des fluides impliquant le vol d'avion s'appuient fortement sur des modèles phénoménologiques réglés par l'expérience
Je répondrai en reprenant ces points tour à tour.
L'expérience est reine
D'un point de vue expérimental particulier , il n'y a pas de mystère sur la raison pour laquelle les avions volent. Au contraire, la meilleure question, à mon avis, est "comment contrôlent-ils les énormes forces de portance inévitables sur eux pour que ces derniers se soulèvent de manière stable dans une direction verticale constante?"
Cette vue expérimentale est la suivante: pensez à l ' échelle de Beaufort et aux autres échelles utilisées par les météorologues pour comprendre la signification pratique de leur vent et autres avertissements: par exemple l' échelle de Fujita pour les tornades et les systèmes de catégories de cyclones tropicaux, qui décrivent en termes pratiques les effets des tempêtes de diverses intensités.
Maintenant, je comprends que les règlements de vol interdisent aux avions de ligne commerciaux de voler à moins de 300 $ \ mathrm {km \, h ^ {- 1}} $ avant leur approche finale de la piste. Pensez à une vitesse de 300 $ \ mathrm {km \, h ^ {- 1}} $ en fonction des échelles dont je viens de parler: il s'agit d'une tornade F4, cyclone de catégorie 5 et bien en dehors de l'échelle de Beaufort en 12 classes. Les bâtiments et les structures de toute forme, de la taille et du poids des avions entièrement chargés, sont déchirés et emportés dans le ciel ou complètement démolis et détruits. Il n'y a PAS de pénurie de portance à partir d'une vitesse relative de 300 $ \ mathrm {km \, h ^ {- 1}} $ pour contenir presque tout ce qui a la taille et le poids d'un avion de ligne commercial entièrement chargé: à ces vitesses, presque tout de cette taille et poids et des mouches plus légères. Au moins, il le fait de manière fugitive: s'il n'est pas conçu comme un avion, au fur et à mesure qu'il bouge, son attitude change, tout comme la direction de la pression du bélier: il est alors susceptible d'être retourné et précipité de manière catastrophique au sol. En termes simples: presque tout vole à cette vitesse, mais seules des choses très spéciales le font de manière stable.
Modèles mathématiques simples
Nous pouvons faire un retour de la estimation de l'enveloppe de la pression du bélier dans ce cas: voir mon dessin ci-dessous d'un profil aérodynamique simple avec un angle d'attaque important maintenu immobile dans une soufflerie. Je vais mettre quelques chiffres à la description de Sklivvz:
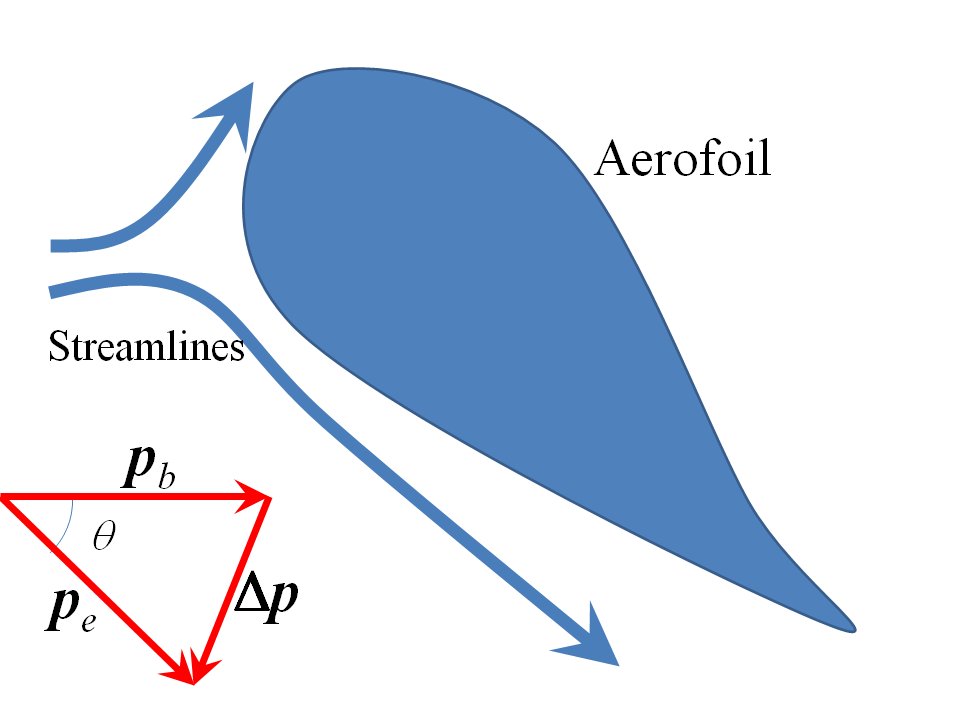
Supposons que le flux d'air soit dévié selon un certain angle $ \ theta $ radians pour modéliser l'attitude d'un avion (pas l'altitude!) lors de sa dernière approche à l'atterrissage ou au décollage, volant à 300 $ \ mathrm {km \, h ^ {-1}} $ vitesse air ou environ 80 $ \ mathrm {m \, s ^ {- 1}} $. Je l'ai dessiné avec un angle d'attaque raide. L'air proche de la pression atmosphérique au niveau de la mer a une densité d'environ 1,25 $ \ mathrm {kg \, m ^ {- 3}} $ (volume molaire de 0,0224 $ \ mathrm {m ^ {- 3}}) $. Le diagramme de changement de moment est montré, d'où le changement des composantes de moment vertical et horizontal (en supposant que la vitesse de l'écoulement reste à peu près constante):
$$ \ Delta p_v = p_b \ sin \ theta; \ quad \ quad \ Delta p_h = p_b \, (1- \ cos \ theta) $$
En même temps, l'aile déflectrice présente une zone de blocage efficace au fluide de $ \ alpha \, A \ , \ sin \ theta $ où $ A $ est la surface réelle de l'aile et $ \ alpha $ un facteur d'échelle pour tenir compte du fait qu'en régime permanent, non seulement le fluide juste à côté de l'aile est distillé de sorte que la surface effective de l'aile être plus grand que sa superficie réelle. Par conséquent, la masse d'air déviée chaque seconde est $ \ rho \, \ alpha \, A \, v \, \ sin \ theta $ et la portance $ L $ et traînée $ D $ (ce qui force les moteurs doivent se permettre au décollage ) doit être:
$$ L = \ rho \, \ alpha \, A \, v ^ 2 \, (\ sin \ theta) ^ 2; \ quad \ quad D = \ rho \, \ alpha \, A \, v ^ 2 \, (1- \ cos \ theta) \, \ sin \ theta $$
Si on branche un angle d'attaque de 30 degrés, on suppose $ \ alpha = 1 $ et on utilise $ A = 1000 \ mathrm {m ^ 3} $ (à peu près le chiffre pour une aile d'Airbus A380), on obtient une force de levage $ L $ pour $ \ rho = 1,25 \ mathrm {kg \, m ^ {- 3}} $ et $ v = 80 \ mathrm {m \, s ^ {- 1}} $ de 200 tonnes de poids. C'est plutôt moins que la masse au décollage d'un Airbus A380 entièrement chargé (qui est de 592 tonnes, selon la page Wikipedia A380) mais c'est une masse étonnamment élevée tout de même et dans le bon ordre de ordre de grandeur. Comme je l'ai dit, l'expérience est reine ici. Nous voyons que la section verticale effective de l'aile est plus grande que l'aile réelle d'un facteur 2 à 3. Cela n'est pas surprenant à l'état d'équilibre, bien en dessous de la vitesse du flux sonore: le fluide se gonfle et la perturbation est beaucoup plus grande que juste dans le quartier de l'aile. Donc, en branchant un $ \ alpha = 3 $ (étant donné le fait expérimental que l'A380 peut décoller à 592 tonnes de poids brut en charge), nous obtenons une traînée $ D $ de 54 tonnes de poids (538 kN) - environ la moitié de l'Airbus. pleine poussée de 1,2MN, donc cela correspond bien aux spécifications réelles de l'Airbus, étant donné qu'il doit y avoir une marge confortable pour sortir l'avion de la difficulté en cas de besoin.
Dans ces vents de niveau F4 / C5 (et jusqu'à trois fois plus rapide en vol normal), on voit donc qu'il n'y a tout simplement pas de pénurie de portance. Le problème de l'ingénierie aéronautique consiste davantage à maintenir cette portance abondante dirigée de manière stable vers le haut et à permettre à l'avion de conserver une assiette stable et d'empêcher tout couple résultant de la non-uniformité de portance de renverser l'avion.
Au fur et à mesure que l'avion prend de la vitesse, la pression du bélier calculée ci-dessus est proportionnelle au carré de la vitesse anémométrique (voir ma réponse à Force de traînée à haute vitesse), de sorte qu'à pleine vitesse l'effet plus qui tient compte de la baisse de la densité de l'air et de l'angle d'attaque moins profond - nous ne pouvons pas faire cette pression de bélier vers le bas sans surmonter la composante arrière horizontale beaucoup plus grande - la traînée - il est donc important de voler avec un faible angle d'attaque pour un bon rendement énergétique.
Affiner le modèle mathématique
Il est important de noter que la description ci-dessus en termes de différence de quantité de mouvement entre l'air entrant et le downwash engendré par l'aile est exactement la même physique comme les descriptions "plus populaires" données en termes de l'équation de Bernoulli et de l'intégration de la pression autour de l'aile. C'est facile à voir: l'équation de Navier-Stokes ( Voir la page Wikipédia pour la dérivation de l'équation de Navier-Stokes), est une application très simple de rien de plus que Les deuxième et troisième lois de Newton aux volumes infinis de fluide de fluide, malgré le manque de connaissances sur ses propriétés mathématiques fondamentales (comme le dit le statut non réclamé du Clay Mathematics Millenium Prize: J'adore l'équation de Navier-Stokes - une idée si simple et facile à saisir si chauve juste une incarnation des lois de Newton, tout en jetant de profonds mystères qui nous montrent à nous les scientifiques à quel point nous en savons encore peu sur le monde) L'équation de Navier Stokes en régime permanent pour un fluide parfait incompressible est (ici $ \ vec {v} $ est le champ de vitesse en régime permanent et $ p $ le champ de pression scalaire):
$$ (\ vec {v} \ cdot \ nabla) \ vec {v} = \ nabla \ left (\ frac {| \ vec {v} | ^ 2} {2} \ right) + \ nabla \ wedge (\ nabla \ wedge \ vec {v}) = - \ nabla p $$
ce qui donne $ \ nabla \ left (p + \ frac {| \ vec {v} | ^ 2} {2} \ right) = 0 $ ou $ p + \ frac {| \ vec {v} | ^ 2} {2} = \ text {const} $ pour un flux irrotationnel ($ \ nabla \ wedge \ vec {v} = \ vec {0} $) lorsqu'il est intégré le long de la courbe intégrale de $ \ vec {v} $, c'est à dire une rationalisation. Ou, alternativement, nous pouvons argumenter d'une manière plus fondamentale dans ce cas simple: la force sur un volume infini est $ - \ nabla p $ et l'accélération d'une particule sur la ligne de courant est, par application des formules de Serret-Frenet (ici $ s $ est la longueur de l'arc le long de la ligne de courant passant par la particule et $ \ kappa $ la courbure du chemin):
$$ \ mathrm {d} _t (v \ hat {\ mathbf {t} }) = \ mathrm {d} _s v \ times \ mathrm {d} _t s \, \ hat {\ mathbf {t}} + v \, \ mathrm {d} _s (\ hat {\ mathbf {t}} ) \, \ mathrm {d} _t s = v \, \ mathrm {d} _s v, \ hat {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf {n}} = \ mathrm {d} _s \ left (\ frac {v ^ 2} {2} \ right) \, \ hat {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf { n}} $$
d'où, en appliquant $ \ vec {F} = m \ vec {a} \ Rightarrow - \ nabla p \, \ mathrm {d} x \, \ mathrm {d} y \, \ mathrm {d} z = \ rho \, \ vec {a} \, \ mathrm {d} x \, \ mathrm {d} y \, \ mathrm {d} z $, on obtient:
$$ - \ nabla p = \ rho \ left (\ mathrm {d} _s \ left (\ frac {v ^ 2} {2} \ right) \, \ hat {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf {n}} \ right) $$
ce qui donne à nouveau $ p + \ frac {| \ vec {v} | ^ 2} {2} = const $ lorsqu'il est intégré le long d'une ligne de courant (ici nous pouvons voir la force centripète latérale (normale à rationaliser) $ -v ^ 2 \, \ hat {\ mathbf {n}} / R $ donné par la formule habituelle $ v ^ 2 / R $). Ainsi, nous pouvons (et nous le ferons, ci-dessous), par exemple, appliquer le Théorème de Blasius pour calculer la portance, et soyez assurés que ce n’est rien de plus qu’une quantification de l’idée de Sklivv que «les avions poussent l’air vers le bas, donc l'air pousse les avions vers le haut ". La différence de pression entre la surface supérieure et inférieure d'une aile existe parce que l'aile pousse l'air vers le bas, ce n'est pas un phénomène distinct. On entend souvent dire que le principe de Bernoulli appliqué aux ailes est faux: ce n'est pas vrai. Il y a une erreur (à discuter ci-dessous) comme le montre l'expérience (et, en agitant la main, par la théorie) dans la démonstration habituelle de l'ascenseur utilisant le principe de Bernoulli, mais l'idée est fondamentalement saine, car elle doit l'être de sa dérivation du Equation de Navier-Stokes et lois de Newton illustrées ci-dessus.
Calcul de la voilure de Joukowsky et erreurs dans l'application habituelle du principe de Bernoulli aux ailes
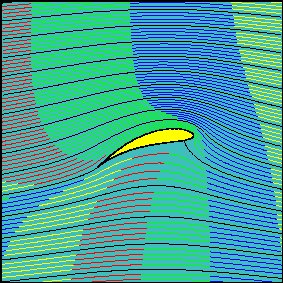
Nous regardons un calcul 2D de portance par le principe de Bernoulli, ou, de manière équivalente, par application du Théorème de Blasius. L'idée fausse commune ici est que les flux d'air se divisent au bord d'attaque de l'aile et que deux particules voisines atteindront le bord de retard de l'aile en même temps, de sorte que les particules supérieures doivent supporter la surface incurvée à des vitesses plus élevées et donc la pression sur la surface supérieure de l'aile. est moins. En fait, les particules de trajectoire supérieure sont beaucoup plus accélérées que cette explication ne le laisse entendre et atteignent le bord en retard de l'aile bien avant leurs voisins de trajectoire inférieure. Regardez cette magnifique vidéo de l ' Université de Cambridge, en particulier à environ 50 secondes. Cela montre que la diffusion $ \ oint_ \ Gamma \ vec {v} \ cdot \ mathrm {d} \ vec { r} $ autour de la surface de l'aile $ \ Gamma $ est non nul, un fait que nous attendons intuitivement d'une théorie simple (comme montré ci-dessous) et qui est amplement confirmé par l'expérience: voir la vidéo, ou aller au bout d'une piste d'un grand aéroport par temps humide afin que vous puissiez laisser de gros avions de ligne commerciaux voler au-dessus de vous à environ 50 m de hauteur (prenez vos cache-oreilles). Par temps humide, vous verrez des tourbillons briser les bords extérieurs des ailes, les verrez tourbillonner dans l'air humide pendant plusieurs secondes dans le sillage de l'avion et, si vous enlevez votre protection auditive après le passage de l'avion, vous entendrez les vortex crépitant dans l'air, sonnant un peu comme des vagues se lavant sur la plage. C'est beaucoup plus amusant que cela en a l'air lorsque vos enfants vous harcèlent pour faire une telle chose et, grâce aux images et aux sons, j'ai appris beaucoup plus en le faisant que je pensais le faire. Même si le calcul suivant a un air de justesse théorique et de «premiers principes», il est important de comprendre qu'il s'agit aussi d'un modèle expérimental : la circulation est forcée dans notre description, motivée par le confirmation de l'existence du premier par l'expérience. La condition de Kutta-Joukowski (voir la page Wikipédia pour la condition de Kutta) ainsi que la page Wikipédia du théorème de Kutta-Joukowski ne sont guère plus qu'une solution ad hoc motivée par l'expérience : c'est simplement ceci. Lorsque nous modélisons le flux avec une voilure Joukowski (décrit ci-dessous), il y a un bord pointu et retardé sur l'aile. Cela engendre une singularité avec des vitesses infinies et non physiques. Cependant, en postulant et en choisissant la bonne circulation dans l'écoulement, nous pouvons mettre un point de stagnation au bord de retard, annulant ainsi la singularité, régularisant notre solution et forçant également la condition expérimentalement observée qu'il n'y a jamais qu'un seul point de stagnation au niveau de l'aile. de pointe, jamais ailleurs.
Une autre façon de voir cette condition motivée expérimentalement est bien expliquée dans cette réponse à la question de Physics SE Une aile dans un flux potentiel a-t-elle de la portance?. Un écoulement irrotationnel, non visqueux, incompressible ne peut à lui seul lever une aile. Nous ajoutons la circulation au "fudge" pour compenser ce manque théorique: la viscosité est "la manière naturelle de faire respecter la condition de Kutta-Joukowsski".
Nous commençons donc par la méthode des variables complexes (voir Wikipedia page "Flux potentiel" dans la section "Analyse de flux bidimensionnel" pour étudier un flux potentiel ie champ de vitesse irrotationnel ($ \ nabla \ wedge = \ vec {0} $) $ \ vec {v} $ avec un potentiel $ \ psi $ tel que $ \ vec {v} = - \ nabla \ psi $ qui est également incompressible (équation de continuité $ \ nabla \ cdot \ vec {v} = \ nabla ^ 2 \ psi = 0 $ ). Voir aussi les questions de Physics SE Trouver des points de stagnation à partir du potentiel complexe).
La méthode principale ici est d'utiliser la transformation de Joukowski:
$ $ \ omega (z, \, s_z, \, s_ \ omega) = \ frac {s_ \ omega} {2} \ left (\ frac {z} {s_z} + \ frac {s_z} {z} \ right) $$
pour cartographier le flux potentiel correspondant à un cylindre décalé en rotation ( voir la page NASA «Levée d'un cylindre en rotation») dans le flux autour de l'image de ce cylindre sous la transformée de Joukowsky. vraiment étrange, Flettner Airplane utilisait en fait des cylindres en rotation plutôt que des ailes pour voler avec succès. La transformation de Joukowsky cartographie le cercle $ | z | = s_z $ sur l’axe réel entre les points $ \ omega = \ pm s_ \ omega $ dans le plan $ \ omega $; cette section de l'axe réel entre $ \ omega = \ pm s_ \ omega $ est alors la branche coupée pour la transformée de Joukowski inverse. La transformée de Joukowsky est un mapping deux à un, et les branches de la transformée inverse de Joukowski mappent la sphère entière $ \ omega $ -Riemann (si nous définissons la projection stéréographique de telle sorte que $ | z | = s_ \ omega $ est l'équateur de la sphère $ \ omega $ -Riemann) séparément à l'intérieur et à l'extérieur du cercle $ | z | = s_z $ dans le plan $ z $ (qui à l'extérieur et à l'intérieur peut être considéré comme les hémisphères nord et sud de la sphère $ z $ -Riemann, si la projection stéréographique est choisie de telle sorte que le cercle $ | z | = s_z $ est l'équateur de la sphère $ z $ -Riemann). La surface $ \ omega $ -Riemann est faite en coupant deux copies de la sphère de Riemann le long de la branche coupée et en cousant les bords ensemble, pour obtenir une double couverture de genre naught pour la sphère $ \ omega $ -Riemann. Pour ce problème, je définis la coupe de branche comme légèrement différente de la section de l'axe réel entre le $ \ pm s_ \ omega $, je la définis comme le chemin:
$$ \ operatorname {Im} (\ omega) = h \ cos \ left (\ frac {\ pi} {2} \ operatorname {Re} (\ omega) \ right) $$
entre les deux points de branchement avec un paramètre de hauteur réglable $ h $, pour des raisons qui deviendront claires.
Le rayon $ r $ du rayon du cylindre en rotation est choisi de telle sorte que la surface du cylindre passe par le point $ z = + s_z $, qui est le image d'un des points de branchement dans le plan $ \ omega $. Cela permet d'obtenir le bord tranchant qui devient le bord en retard de notre voilure.
Le potentiel complexe du cylindre en rotation est:
$$ \ Omega (z) = v \, e ^ {- i \ alpha} \, \ left (z- \ delta \ right) + \ frac {r ^ 2 \, v \, e ^ {+ i \ alpha}} {z- \ delta} + i \, a \, \ log \ left (z - \ delta \ right) $$
où $ \ alpha $ est l'angle d'attaque, $ \ delta = \ delta_r + i \, \ delta_i $ est le décalage et $ r $ est le rayon du cylindre plongé dans un écoulement uniforme qui converge vers $ v $ mètres par seconde le long de l'axe réel positif, comme $ z \ to \ infty $. Les termes logarithme et dipôle placent un point de branchement et un pôle au centre du cylindre, de sorte que l’écoulement est parfaitement valable à l’extérieur et sur le cylindre. $ a $ est la diffusion. Si nous laissons $ \ phi $ représenter la coordonnée angulaire marquant le bord du cylindre, il y a deux points de stagnation sur le cylindre avec des coordonnées angulaires $ \ phi_ \ pm $ où $ \ mathrm {d} _z \ Omega (z ) = 0 $, ie quand:
$$ e ^ {i \, (\ phi_ \ pm - \ alpha)} = -i \ frac {a} {2 \, v \, r} \ pm \ sqrt {1- \ left (\ frac {a} {2 \, v \, r} \ right) ^ 2} = \ exp \ left (- \ arcsin \ frac {a } {2 \, v \, r} \ right) $$
Maintenant, nous mappons ce flux sur le plan $ \ omega $ et appliquons le Théorème de Blasius au image du cercle décalé pour calculer la portance sur cette image. L'image peut être tracée avec la commande Mathematica:
$$ \ small {\ mathrm {P [\ delta_r \ _, \ delta_i \ _]: = \\ ParametricPlot [\ {Re [\ omega [ \ delta_r + i \ delta_i + \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} Exp [i \ theta]], Im [\ omega [\ delta_r + i \ delta_i + \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} Exp [i \ theta]] \}, \ {\ theta, 0, 2 \ pi \}]}} $$
et le résultat est dessiné ci-dessous dans le plan $ \ omega $ pour $ s_z = s_ \ omega = 1 $, $ \ delta_r = -0.1 $, $ \ delta_i = 0.3 $ ( ie le cercle tournant est décalé de telle sorte que son le centre est à $ -0,1 + i \, 0,2 $ et avec un rayon $ r = \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} $ de sorte que son image passe par le point de branchement $ \ omega = + s_ \ omega = 1 $ dans le plan $ \ omega $:

Nous arrivons maintenant au postulat crucial de Kutta-Joukowski, un "fudge" expérimental. Le bord pointu sur la voilure ci-dessus cartographierait normalement le flux dans le plan $ z $ de sorte qu'il y ait une vitesse infinie non physique à ce point aigu. En pratique, on voit dans les essais en soufflerie que les lignes de courant restent tangentes à la surface supérieure, et qu'il y a un point de stagnation au bord d'attaque de l'aile (intuitivement l'air "s'écrase" ici) et aucun autre des points de stagnation en haut ou en bas de l'aile. Parfois, il y a une petite région de turbulence autour du bord en retard de l'aile (comme dans la vidéo de l'Université de Cambridge) (c'est-à-dire que le modèle d'écoulement potentiel incompressible échoue ici) ou l'écoulement se décolle doucement du bord en retard. La façon dont nous obtenons des effets similaires à l'expérience et «renormalisons» notre solution consiste à ajouter la bonne quantité de circulation $ a $ au flux afin que l'un des points de stagnation sur le cylindre en rotation soit mappé sur l'arête vive (le point de branche à $ \ omega = + s_ \ omega $) dans le plan $ \ omega $: la stagnation y annule donc les vitesses infinies autrement non physiques et "régularise" notre solution. Avec le rayon du cylindre choisi comme $ r = \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} $, il peut facilement être montré à partir de l'équation ci-dessus pour les positions des points de stagnation que la circulation nécessaire est:
$$ a = 2 v \, \ delta_i \ cos \ alpha + 2 \, v \, (1- \ delta_r) \ sin \ alpha $$
Telle est donc la condition de Kutta-Joukowski entièrement motivée par l'expérience. Il est motivé par la connaissance que la circulation est observée autour des ailes, il n'y a expérimentalement qu'un seul point de stagnation sur le bord d'attaque de l'aile et le fait que la bonne quantité de circulation peut reproduire ces résultats observés expérimentalement.
Lorsque cela est fait, le calcul de la portance du théorème de Blasius effectué autour de la voilure de Joukowski transformée dans le plan $ \ omega $ est:
$$ \ begin {array} {lcl} D_ \ ell - i \, L_ \ ell & = & \ frac {i \, \ rho} {2} \ oint _ {\ Gamma_ \ omega} (\ mathrm { d} _ \ omega \ Omega) ^ 2 \, \ mathrm {d} \ omega \\ & = & \ frac {i \, \ rho} {2} \ oint _ {\ Gamma_z} (\ mathrm {d} _z \ Omega) ^ 2 \ frac {1} {\ mathrm {d} _z \ omega} \, \ mathrm {d} z \\ & = & - \ pi \, \ rho \ Sigma [\, \ mathrm {résidus \, de \,} \, (\ mathrm {d} _z \ Omega) ^ 2 \ frac {1} {\ mathrm {d} _z \ omega} \, \ mathrm {at \, poles \, within \,} \ Gamma ] \\ & = & -4 \, \ pi \, i \, \ rho \, a \, v \, e ^ {- i \, \ alpha} \ end {array} $$
où $ \ Gamma_ \ omega $ est la voilure Joukowski et $ \ Gamma_z $ la voilure transformée ( ie le cylindre en rotation). Il n'y a donc pas d'ascenseur sans circulation. Cela vaut la peine de le répéter:
Un flux irrotationnel, non visqueux et incompressible ne peut pas à lui seul lever une aile. Nous ajoutons la circulation au "fudge" pour compenser ce manque théorique: la viscosité est "la manière naturelle d'appliquer la condition de Kutta-Joukowsski".
Maintenant, nous substituons la condition de Kutta-Joukowski pour obtenir:
$$ D_ \ ell + i \, L_ \ ell = 8 \, \ pi \, i \, \ rho \, v ^ 2 \, \ left (\ delta_i \, \ cos \ alpha + (1- \ delta_r) \, \ sin \ alpha \ right) \ frac {s_z ^ 2} {s_ \ omega} e ^ {+ i \ alpha} $$
Nous devons maintenant mettre à l'échelle les vitesses pour que les vitesses relatives soient égales dans les avions $ \ omega $ - et $ z $.
Ce qui précède est la force par unité de longueur (dans la direction normale à la page) sur l'aile et sa direction est la direction dans le plan $ \ omega $. Nous avons:
$$ \ lim \ limits _ {\ omega \ to \ infty} \ left (\ mathrm {d} _ \ omega \ Omega (\ omega (z)) \ right) = \ lim \ limits_ {z \ to \ infty} \ left (\ mathrm {d} _z \ Omega (\ omega (z)) \ right) \ lim \ limits _ {\ omega \ to \ infty} \ left (\ mathrm {d} _ \ omega z \ right) = 2 \, e ^ {- i \ alpha} v \ frac {s_z} {s_ \ omega} $$
donc nous avons besoin de $ s_ \ omega = 2 $ et $ s_z = 1 $, alors $ \ delta $ sera un paramètre sans dimension définissant le décalage du cylindre du plan $ z $ comme une fraction de son rayon. Mais maintenant, la largeur de plan de l'aile $ \ omega $ -plane est de 4 unités. De plus, le calcul ci-dessus donne la force par unité de longueur (normale à l'écoulement 2D). Nous divisons donc le résultat pour $ s_ \ omega = 2 $ et $ s_z = 1 $ par 4, puis augmentons l'échelle par la surface totale de l'aile pour obtenir la force totale sur l'aile. De plus, nous devons faire pivoter le flux dans l'esquisse ci-dessous pour que le flux entrant soit horizontal (c'est-à-dire dans la direction de la vitesse relative de l'air de l'avion) dans la force totale $ \ omega $ sur l'aile ci-dessus devient:
$$ D + i \, L = \ pi \, i \, \ rho \, v ^ 2 \, A \, \ left (\ delta_i \, \ cos \ alpha + (1- \ delta_r) \, \ sin \ alpha \ right) $$
On assiste au paradoxe d'Alembert: l'écoulement parfait ne peut pas modéliser la traînée. Maintenant, mettons quelques nombres. Si nous mettons $ \ delta = 0 $, alors l'aile est simplement la branche droite coupée entre $ \ omega = \ pm 1 $, nous avons donc une version du calcul avec laquelle j'ai commencé mais maintenant affinée pour tenir compte du modèle de flux complet. Avec $ \ alpha = 0,3 $ (un peu moins de 20 degrés), $ \ rho = 1,25 \ mathrm {kg \, m ^ {- 3}} $, $ v = 80 \ mathrm {m \, s ^ {- 1}} $ et $ A = 850 \ mathrm {m ^ 2} $, nous obtenons $ L = 643 \ mathrm {tonne} $, assez proche de la masse au décollage entièrement chargée de l'Airbus. Si nous avons choisi les paramètres $ \ delta_i = 0.2 $, $ \ delta_r = -0.1 $ pour donner une forme d'aile qui ne semble pas trop fantaisiste pour une aile d'avion de ligne avec les volets de bord en retard complètement enroulés pour le décollage et l'atterrissage (voir le graphique ci-dessous) nous obtenons une portance d'environ 1 200 tonnes pour notre vitesse de 300 $ \ mathrm {km \, h ^ {- 1}} $. Il est clair que c'est optimiste et que le surfaçage découle de l'hypothèse d'une efficacité égale de toute l'envergure, alors que les pointes ne seront clairement pas bien modélisées par un écoulement 2D. Toutes les ailes ne fonctionneront pas comme modélisées, donc le $ A $ dans cette formule est quelque peu inférieur à la surface de la forme en plan. Ce que montre le modèle d'écoulement (voir ci-dessous), cependant, c'est que la section verticale effective présentée à l'air entrant est beaucoup plus grande que la zone inclinée $ A \, \ sin \ theta $ supposée dans le modèle très simple au début de ma réponse. À l'état d'équilibre, une section transversale considérable de l'air à la fois au-dessus et en dessous de la section verticale est pliée vers le bas et contribue à l'effet "les avions poussent l'air vers le bas, de sorte que l'air pousse les avions vers le haut" décrit dans la réponse de Sklivv.
Maintenant, pour tracer le flux transformé complet dans le plan $ \ omega $, nous devons utiliser la transformée de Joukowski inverse. Pour réussir, il faut utiliser les bonnes branches de la transformée inverse dans les bons patchs de coordonnées. Pour Mathematica, qui place la branche coupée pour la fonction racine carrée le long de l'axe réel négatif (l'espace de noms std :: sqrt dans Microsoft Visual C ++ le place le long de l'axe réel positif ), nous définissons les fonctions de graphique suivantes, qui sont des branches particulières de la transformation inverse:
$$ \ zeta_1 (\ omega) = \ frac {s_z} {s_ \ omega} \ left (\ omega- i \ sqrt {\ omega-s_ \ omega} \, \ sqrt {- \ left (\ omega + s_ \ omega \ right)} \ right) $$$$ \ zeta_2 (\ omega) = \ frac {s_z} { s_ \ omega} \ left (\ omega + i \ sqrt {\ omega-s_ \ omega} \, \ sqrt {- \ left (\ omega + s_ \ omega \ right)} \ right) $$$$ \ zeta_3 (\ omega) = \ frac {s_z} {s_ \ omega} \ left (\ omega- \ sqrt {\ omega ^ 2-s_ \ omega ^ 2} \ right) $$$$ \ zeta_4 (\ omega) = \ frac { s_z} {s_ \ omega} \ left (\ omega + \ sqrt {\ omega ^ 2-s_ \ omega ^ 2} \ right) $$
puis les commandes Mathematica suivantes traceront le flux complet:
$$ \ small {\ mathrm {\ Omega [z \ _, \, \ delta \ _, \, v \ _, \, r \ _, \, a \ _, \, \ alpha \ _, \, s \ _]: = v \, e ^ {- i \, \ alpha} \ left (\ frac {z} {s} - \ delta \ right) + \ frac {r ^ 2 \ , v \, e ^ {i \, \ alpha}} {\ frac {z} {s} - \ delta} + i \, a \, Log \ left [\ frac {z} {s} - \ delta \ right]}} $$$$ \ small {\ mathrm {G [z \ _, \, \ delta_r \ _, \, \ delta_i \ _, \, \ alpha \ _]: = \ Omega \ left [z, \, \ delta_r + i \, \ delta_i, \, 1, \, \ sqrt {(1- \ delta_r) ^ 2 + \ delta_i ^ 2}, 2 \, \ delta_i Cos [\ alpha] + 2 \, (1- \ delta_r) \, Sin [\ alpha], \, \ alpha, \, 1 \ right]}} $$
$$ \ small {\ mathrm {S [\ delta_r \ _, \ delta_i \ _, \ alpha \ _, h \ _, c \ _]: = \\ Show [ContourPlot [Im [If [(Abs [x] < 1) \ wedge (y > 0) \ wedge (y < h \, Cos [\ pi x / 2]), G [\ zeta_1 [x + iy], \ delta_r, \ delta_i, \ alpha]], If [x < 0, G [\ zeta_3 [x + iy], \ delta_r, \ delta_i, \ alpha]], G [\ zeta_4 [x + iy], \ delta_r, \ delta_i, \ alpha ]]]]], \ {x, -2, 2 \}, \ {y, -2, 2 \}, Contours \ to c, MaxRecursion \ to 2, PlotPoints \ to 300, AspectRatio \ to 1],
P [\ delta_r, \ delta_i, \ {Black, Thick \}]]}} $$
où $ \ mathrm {P} [] $ est la commande de tracé paramétrique ci-dessus utilisée pour tracer la voilure. L'utilisation ci-dessus des fonctions de branche fonctionne pour $ \ delta_r < 0 $: d'autres branches sont nécessaires pour des résultats corrects lorsque $ \ delta_r > 0 $. Le paramètre $ h $ plie la coupe de branche pour qu'elle s'incline vers le haut et reste à l'intérieur de la voilure, permettant ainsi aux branches de la transformée de Joukowsky inverse de tracer correctement le flux de cylindre cartographié. Ci-dessous, le résultat de la commande $ \ mathrm {S [-0,1, 0,2, 0,2, 0,2, 100]} $, ie l'écoulement autour de l'aile pour un angle d'attaque de 0,2 radians les paramètres de décalage du cercle de $ -0,1 + 0,2 \, i $, un arc dans la branche coupée de sorte que $ h = 0,2 $. Observez la branche coupée à l'intérieur de la voilure ci-dessous et aussi à quelle distance de la surface de l'aile son effet s'étire. La composante verticale effective de la surface de l'aile qui est présentée à l'écoulement est clairement beaucoup plus grande que la composante verticale réelle de la surface de l'aile, de sorte que le facteur de mise à l'échelle de 2 à 3 dans la portance de l'Airbus A380 comme calculé par le simple calcul de la déflexion fluide semble très plausible et sans surprise.
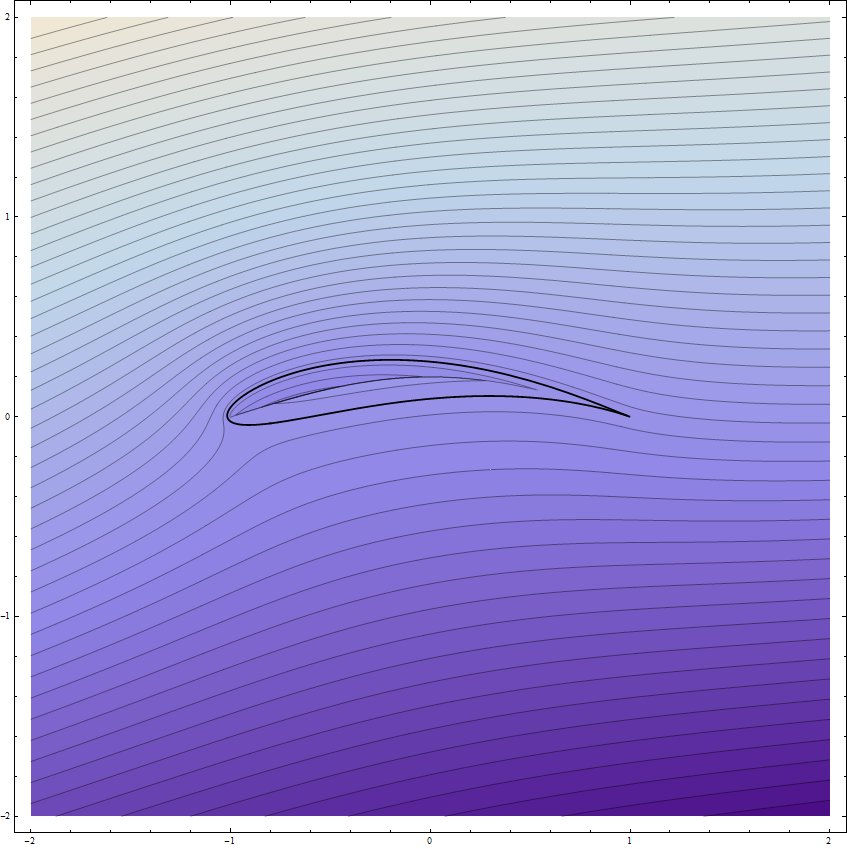
Enfin, pour boucler la boucle, voici une animation à retrouver sur les pages web "Irrotational plane flows of an inviscid fluid" at le département d'ingénierie environnementale de l'Université de Gênes; voir http://www.diam.unige.it/~irro/. L'animation montre la progression des particules fluides pour l'écoulement de la voilure Joukowski, illustre l'affirmation selon laquelle l'écoulement au-dessus de l'aile traverse l'aile beaucoup plus rapidement que l'écoulement en dessous et enfin, montre très bien la thèse principale selon laquelle «les avions poussent l'air vers le bas».