Une indication indirecte que la Terre tourne est le fait que la rotation varie dans le temps. Tout d'abord, l'orientation de l'axe de la Terre change: des effets à long terme comme la précession et des variations lentes de l ' inclinaison axiale, ainsi que de petites variations à court terme comme la nutation . La précession était déjà connue dans le monde antique (Hipparque, Ptolémée, ...) et le changement d'inclinaison axiale a été reconnu par des gens comme Fracastoro (en 1538). Voir les pages du wiki pour le contexte historique.
La période de rotation de la Terre change également. Tout d'abord, la rotation ralentit, causée par l'interaction des marées entre la Terre et la Lune: la durée du jour augmente d'environ 2 millisecondes par siècle. Edmond Halley a été le premier à remarquer que la période orbitale de la Lune avait changé par rapport aux archives anciennes, et cet effet a été expliqué aux XVIIIe et XIXe siècles.
Ces jours-ci, nous sommes capables de mesurer très précisément la rotation de la Terre, et nous constatons que la rotation varie légèrement d'un jour à l'autre. En particulier, les variations des vents atmosphériques et des courants océaniques provoquent des fluctuations périodiques de l'inclinaison axiale et de la période de rotation: une fluctuation annuelle d'une amplitude de 0,34 milliseconde, une période semestrielle d'une amplitude de 0,29 milliseconde, des fluctuations sur 10 jours du ordre de 0,1 milliseconde, fluctuations dues aux événements El Niño, etc. (voir wikipedia, et aussi cet article). Les grands tremblements de terre peuvent également modifier la période de rotation de quelques microsecondes, mais ces effets s'avèrent difficiles à mesurer (voir cet article sur le tremblement de terre de 2011 au Japon).
Ces variations prouvent-elles que la Terre tourne? Pas directement, mais j'aimerais entendre les géocentristes expliquer comment l'univers entier peut changer sa rotation, non seulement sur des milliers d'années mais même au quotidien, lorsque les causes de ces variations peuvent être retracées à des événements sur Terre ou ses environs. orbite.
Une autre preuve que la Terre tourne, même si elle ne peut être mesurée qu'avec des techniques modernes: aberration Vous connaissez tous cet effet: supposez que vous êtes debout sous la pluie, et il n'y a pas de vent. Comme la pluie tombera verticalement, vous devez tenir votre parapluie droit. Mais maintenant, commencez à courir. Ce qui se produit? De votre point de vue, la pluie ne tombera plus verticalement: vous devez incliner votre parapluie vers l'avant pour garder la tête sèche.Un phénomène similaire se produit avec la lumière: la direction dans laquelle vous voyez un faisceau de lumière dépend de votre vitesse. Cet effet est appelé aberration.
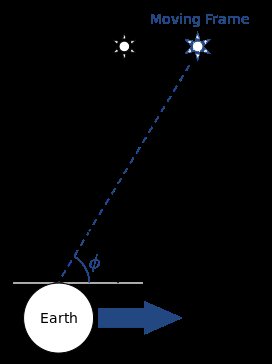
Par exemple, supposons que vous ayez deux étoiles, séparées par un angle $ \ theta $ dans un reste Cadre. Si un observateur se déplace vers l'étoile sur l'axe horizontal, alors il verra la deuxième étoile sous un angle $ \ varphi $, au lieu de $ \ theta $. Si la vitesse de l'observateur change, alors l'angle $ \ varphi $ change, et l'étoile semblera «vaciller» par rapport aux étoiles à différentes positions.
La vitesse orbitale $ v \ approx 30 \ ; \ text {km / s} $ de la Terre autour du Soleil provoque une aberration annuelle : sur la période d'un an, chaque étoile et galaxie semblera osciller sur une ellipse, avec un déplacement maximum de $ v / c \ environ 20,5 '' $ autour de leur position moyenne, quelle que soit leur distance à la Terre (contrairement à la parallaxe, qui dépend de la distance). Il a été observé pour la première fois par James Bradley en 1725 et est la preuve directe que la Terre tourne autour du Soleil.
Mais il y a une autre aberration, beaucoup plus petite: une aberration diurne , causée par la rotation de la Terre autour de son axe. L'effet est le plus grand pour un observateur sur l'équateur, qui a une vitesse équatoriale de $ v = 0,465 \; \ text {km / s} $, tandis qu'un observateur sur les pôles ne verra aucun effet. Pour un observateur sur l'équateur, la position de chaque étoile oscille quotidiennement, avec un déplacement maximum de $ v / c \ environ 0,32 '' $. C'est un effet incroyablement petit, mais il est mesurable, et il doit être pris en compte lors de l'astrométrie de haute précision. De plus, cela prouve que la Terre tourne.