Je recommanderais d'éviter les coordonnées de Schwarzschild pour ce genre de questions. Tous les infinis classiques (c'est-à-dire le paradoxe du pare-feu mis à part) ayant à voir avec l'horizon des événements sont dus à de mauvais choix de coordonnées. Vous souhaitez utiliser un système de coordonnées régulier à l'horizon, comme Kruskal-Szekeres. En effet, jetez un œil au diagramme de Kruskal-Szekeres:

(source: Wikipedia)

Il s'agit de la géométrie de Schwarschild étendue au maximum, pas d'un trou noir physique se formant à partir d'étoiles s'effondrer, mais les différences ne devraient pas nous déranger pour cette question. Les régions I et III sont des régions asymptotiquement plates, II est l'intérieur du trou noir et IV est un trou blanc. Les hyperboles audacieuses des régions II et IV sont les singularités. Les diagonales passant par l'origine sont les horizons des événements. L'origine (en réalité une sphère à 2 avec des coordonnées angulaires supprimées) est la gorge d'un trou de ver non traversable joignant les "univers" séparés I et III. Les rayons lumineux radiaux restent des lignes diagonales à 45 degrés sur le diagramme de Kruskal-Szekeres. Les hyperboles en pointillés sont des lignes de coordonnée Schwarzschild $ r $ constante, et les rayons radiaux en pointillés sont des lignes de constante $ t $. Vous pouvez voir comment l'horizon des événements devient une singularité de coordonnées où $ r $ et $ t $ changent de rôle.

Maintenant, si vous tracez une ligne du monde de la région I à la région II, il devient évident qu'elle traverse l'horizon en temps propre fini et, plus important encore, le cône de lumière passé de l'événement où il atteint la singularité ne peut pas contenir l'espace-temps entier. Donc, la réponse courte à votre question est non , quelqu'un qui tombe dans un trou noir ne voit pas la fin de l'univers. Je ne connais pas la formule que vous demandez pour $ T $, mais en principe, vous pouvez la lire à partir des rayons lumineux sur le diagramme et simplement la convertir en coordonnée / heure appropriée que vous souhaitez utiliser.

Ceci est une réécriture de la réponse de Michael Brown pour m'aider à clarifier mes pensées, et peut-être pour aider tous ceux qui sont intéressés à clarifier leurs pensées aussi :-) Michael présente une réponse à ma question basée sur la géométrie de l'espace-temps autour du trou noir.

Le point clé est que les coordonnées habituelles de Schwarzschild rayon / temps sont inutiles car elles obscurcissent ce qui se passe. Pour contourner cela, nous utilisons une transformation de coordonnées pour dessiner l'espace-temps autour du trou noir en utilisant les coordonnées Kruskal-Szekeres $ u $ et $ v $. Voici à quoi ressemble le résultat:

La coordonnée $ u $ est horizontale et la coordonnée $ v $ est verticale.

Le problème avec ces coordonnées sont qu'elles sont très peu intuitives. Un déplacement dans $ u $ ou $ v $ ne correspond à aucune grandeur physique simple, contrairement à un déplacement dans la coordonnée radiale usuelle $ r $ ou la coordonnée temporelle $ t $. Néanmoins, les coordonnées KS simplifient considérablement les choses comme suit:

Dans ces coordonnées, la constante $ r $ est une hyperbole comme le montre la ligne en pointillés. L'horizon des événements est la ligne pleine à 45 °. Vous pouvez en quelque sorte penser que $ t $ augmente au fur et à mesure que vous progressez - c'est le cas, mais pas de manière linéaire. La singularité est l'hyperbole rouge (il s'agit d'un diagramme d'espace-temps rappelez-vous, donc la singularité est une courbe et non un point). La région que j'ai étiquetée $ I $ est l'extérieur du trou noir et la région que j'ai étiquetée $ II $ est la région à l'intérieur de l'horizon des événements. Ignorez la région du diagramme en bas à gauche car elle n'est pas pertinente pour ma question.

Enfin, la caractéristique clé qui permet de répondre à ma question est que tous les rayons lumineux radiaux entrants sont droits 45 ° lignes allant du bas à droite vers le haut à gauche. J'ai dessiné plusieurs rayons lumineux tels que des lignes magenta.

Nous pouvons maintenant répondre à ma question. Nous commençons par une fusée planant à une distance constante du trou noir, qui est représentée par l'hyperbole en pointillé noir de $ r $ constant (comme je l'ai mentionné ci-dessus, vous pouvez en quelque sorte penser au temps qui augmente à mesure que vous avancez). Au temps $ t_0 $, notre observateur quitte la fusée et commence à tomber vers le trou noir. La ligne bleue montre la trajectoire suivie par l'observateur. L'observateur atteint la singularité au point où les lignes bleue et rouge se rencontrent.

Au temps $ t_1 $, la fusée envoie un rayon lumineux sur l'observateur infaillible. Le rayon lumineux, voyageant à 45 °, atteint l'observateur avant qu'il ne traverse l'horizon des événements - jusqu'ici tout va bien. Au temps $ t_2 $, la fusée envoie un second rayon lumineux sur l'observateur, et ce rayon lumineux atteint l'observateur juste au moment où il atteint la singularité. Au temps $ t_3 $, la fusée envoie un troisième rayon lumineux dans le trou noir, mais celui-ci n'atteint pas l'observateur parce que l'observateur a déjà atteint la singularité et n'existe plus. Cela signifie que l'observateur ne voit jamais le rayon lumineux émis au temps $ t_3 $. L'observateur voit tout rayon lumineux libéré entre $ t_0 $ et $ t_2 $, mais ne voit aucun rayon lumineux libéré après $ t_2 $. Ainsi, la ligne magenta pointillée marque la frontière entre les rayons lumineux que l'observateur peut voir et ceux qu'il ne peut pas voir.

Et voici la réponse à ma question. L'observateur ne voit pas la fin de l'univers car le dernier rayon lumineux qu'il voit est celui qui est libéré au temps $ t_2 $.

Cela ne me donne pas un moyen facile pour calculer la valeur de $ t_2 $, car je devrais dériver une expression pour la trajectoire de l'observateur infaillant (ligne bleue) et c'est difficile. Néanmoins, cela montre que $ t_2 $ est fini donc, en utilisant la notation de ma question, $ T $ est borné.

(La réponse de Michael Brown est la bonne réponse et il s'agit simplement d'amplifier via un diagramme ajouté.)

Voici la figure 31.4 de la page 835 de Gravitation (MTW).

Les deux diagrammes sont de la géométrie Schwarzschild. Notez que dans les coordonnées de Kruskal-Szekeres, les cônes de lumière apparaissent comme ils le font dans l'espace-temps de Minkowski.

Comme le souligne Michael, les géodésiques radiales semblables à la lumière sont des lignes à 45 degrés comme on peut le voir en regardant la géodésique B.

De toute évidence, il y a des lignes du monde semblables à la lumière qui traversent l'horizon après quelques lignes du monde semblables au temps, de sorte que la ligne du monde d'un astronaute tombant radialement vers le trou ne coupe pas tous la lumière des lignes du monde radiales avant de traverser l'horizon.

De plus, il est clair qu'il existe des lignes du monde semblables à la lumière qui se terminent sur la singularité après des lignes du monde semblables au temps.

Ainsi, l'astronaute ne voit pas le futur infini avant de traverser l'horizon ou de rencontrer la singularité.

De plus, et ce n'est qu'une remarque intéressante à prendre en compte, la solution de Schwarzschild est la statique (enfin, en dehors de l'horizon au moins) solution aux équations d'Einstein. En d'autres termes, il n'y a pas de "fin de l'univers" dans cette solution .

Je suis d'accord que pour un espace-temps qui est exactement Schwarzschild, l'observateur infaillible ne voit pas toute l'histoire de l'univers. Cependant, ce n'est pas le cas générique auquel on s'attendrait pour un trou noir astrophysique, qui s'est formé à partir de l'effondrement d'une distribution de matière à peu près sphérique. Ce sujet fait actuellement l'objet de recherches actives, et il y a des résultats très intéressants sur ce à quoi ressemble réellement l'intérieur d'un trou noir. Voir, par exemple, cet article récent.

La raison pour laquelle dans Schwarzschild l'observateur infaillible ne voit pas toute l'histoire de l'univers est que la singularité ressemble à un espace. Cela signifie qu'il existe une gamme de points où l'observateur infaillible peut atteindre la singularité, et chaque point ne peut voir qu'une partie de l'univers dans son passé causal.

Mais les gens connaissent depuis longtemps d'autres types de trous noirs qui ne partagent pas ce comportement. Les exemples les plus connus sont la solution Reissner-Nordstrom pour un trou noir chargé à symétrie sphérique et la solution Kerr pour un trou noir en rotation. Ceux-ci ont tous deux des singularités temporelles , et la situation est donc tout à fait différente. Voici un diagramme causal d'un trou noir Reissner-Norstrom:

Les lignes dentelées verticales représentent les singularités temporelles de ce trou noir. Dans ce cas, il est possible d'éviter la singularité et d'émerger dans un nouvel univers que vous pourriez attacher en haut de cette image. Dans ce cas, lorsque vous traversez l'horizon intérieur, vous devriez pouvoir regarder en arrière et voir toute l'histoire ou l'univers.

Cela soulève cependant un point problématique. L'observateur passe l'horizon intérieur en un temps propre fini, mais il est capable de voir toute la lumière qui pénètre dans le trou noir de toute l'histoire infinie de l'univers. Puisque la lumière a de l'énergie, vous pourriez penser que cet amas de rayonnement de l'univers extérieur devrait entraîner une grande courbure, et c'est effectivement le cas. Ceci est connu comme une instabilité d'inflation de masse du trou noir. Les trous noirs de Kerr partagent cette fonctionnalité, bien que la structure de la singularité dans ce cas soit plus compliquée.

Donc, pour les trous noirs génériques qui ne sont pas exactement Schwarzschild, un comportement différent est attendu. Les perturbations ont tendance à changer la singularité du fait d'être spatial pour se comporter comme une surface nulle, c'est-à-dire suivre les trajectoires de la lumière. Une image de l'article ci-dessus montre cette situation:

L'univers extérieur vit dans le triangle inférieur droit de cette image. Les lignes étiquetées $ \ mathcal {CH} ^ + $ sont les singularités nulles. L'article a constaté que cette situation résultait de la perturbation de la solution de Schwarzschild avec de la matière de champ scalaire. Dans ce cas, si vous tombiez dans le trou noir de l'univers extérieur, vous vous heurteriez aux singularités nulles, et en supposant que vous frappiez celle de droite, vous verrez tout l'histoire entière de l'univers, dans le sens où tout cela vous aurez accès à la lumière qui pénètre dans le trou noir des temps arbitrairement tardifs de l'histoire de l'univers.

La réponse actuellement acceptée évite la question sur le calcul des événements qui peuvent réellement être vus en utilisant les coordonnées de Schwarzschild. Il est possible de trouver une réponse à cette question en utilisant les coordonnées de Schwarzschild, à la fois numériquement et analytiquement. La réponse est bien sûr que le cône de lumière passé pour le cas limite n'inclut pas l'univers entier en dehors du trou noir et qu'il y a un temps fini disponible pour signaler à un objet en chute (même en coordonnées Schwarzschild), cela dépend de l'endroit où le l'observateur en chute a été libéré de.

Il y a deux problèmes distincts, chacun avec deux cas distincts. La première consiste à déterminer si la lumière intercepte un observateur qui tombe avant qu'il n'atteigne l'horizon des événements. Cependant, il y a ensuite une petite correction supplémentaire à apporter pour déterminer si un signal lumineux peut encore intercepter un observateur en chute après avoir traversé l'horizon des événements mais avant qu'il n'atteigne la singularité.

1. La lumière peut-elle intercepter un objet avant qu'il n'atteigne l'horizon des événements?

(a) Objet tombant de l'infinity

Je commence par un observateur de rayon $ r_0 $ (tous les rayons sont exprimés en multiples du rayon de Schwarzschild $ r_s $). L'observateur est passé au temps $ t_0 $ (en coordonnées Schwarzschild, qui est égal à $ \ tau = 0 $ selon la propre horloge de l'observateur), par un objet tombant radialement vers l'intérieur vers le trou noir depuis infini (où il a commencé au repos). À un certain moment $ \ Delta t $ plus tard, l'observateur tire un rayon laser radialement vers l'intérieur. Le problème est de calculer le maximum $ \ Delta t $ qui interceptera l'objet tombant et de le convertir ensuite en $ \ Delta \ tau $ en termes de temps propre selon l'observateur. Qu'il doit y avoir un maximum $ \ Delta t $ et $ \ Delta \ tau $ est conceptuellement facilement établi en considérant (par exemple) les coordonnées de Kruskal-Szekeres.

La géodésique nulle (en coordonnées Schwarzschild) que suit la lumière voyageant vers l'intérieur (en unités $ c = 1 $) est: $$ t = -r - r_s \ ln \ gauche | \ frac {r -r_s} {r_0-r_s} \ right | + a + \ Delta t \,, \ tag {1} $$ où la constante $ a = r_0 + t_0 $.

La géodésique suivie d'un corps libéré au repos de l'infini est (par exemple, voir l'équation 25.38 dans "Gravitation" de Misner, Thorner & Wheeler, 2017, Princeton University press) $$ t = r_s \ left (- \ frac {2} {3} \ left (\ frac {r} {r_s} \ right) ^ {3/2} - 2 \ left (\ frac {r} {r_s} \ right) ^ {1/2} + \ ln \ left | \ frac {\ sqrt {r / r_s} + 1} {\ sqrt {r / r_s} -1} \ right | \ right) + b \ tag { 2} $$ La constante $ b $ peut être choisie pour s'assurer que l'objet passe par le point $ (t_0, r_0) $ - ainsi: $$ b = t_0 - r_s \ left (- \ frac {2} {3} \ left (\ frac {r_0} {r_s} \ right) ^ {3/2} - 2 \ left (\ frac {r_0} { r_s} \ right) ^ {1/2} + \ ln \ left | \ frac {\ sqrt {r_0 / r_s} + 1} {\ sqrt {r_0 / r_s} -1} \ right | \ right) \ tag { 3} $$

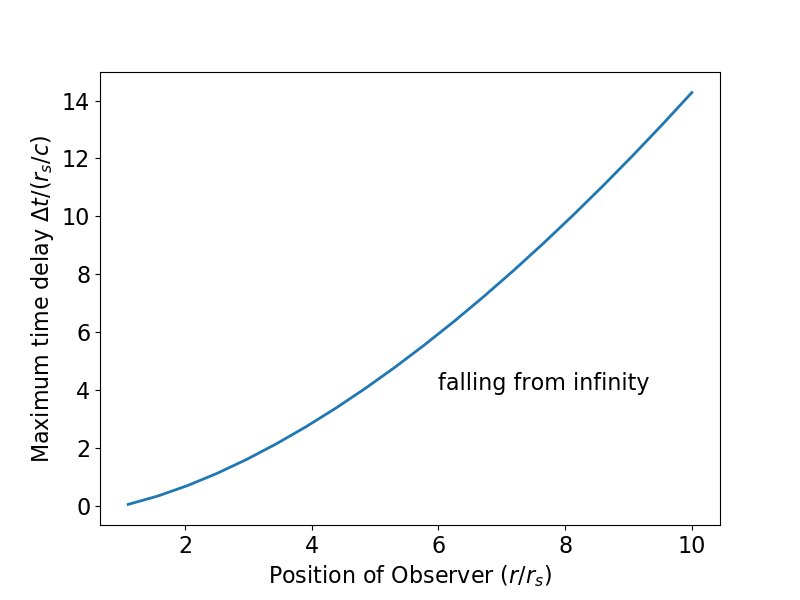
En traçant ces géodésiques et en utilisant une méthode de bissection pour déterminer quand et si elles se croisent, j'ai pu déterminer le maximum $ \ Delta t $ ($ T $ dans l'OP, bien que j'ai commencé mon objet en chute libre depuis l'infini) qui permet toujours à la lumière d'intercepter l'objet en chute en fonction de l'endroit d'où cette lumière est émise. Le résultat semble stable à la réduction de la tolérance (j'ai utilisé $ 10 ^ {- 14} r_s $).

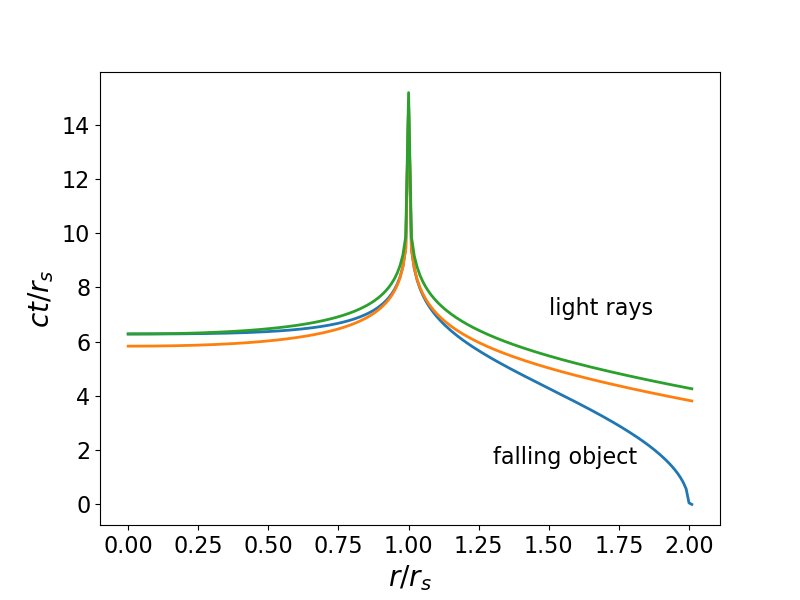
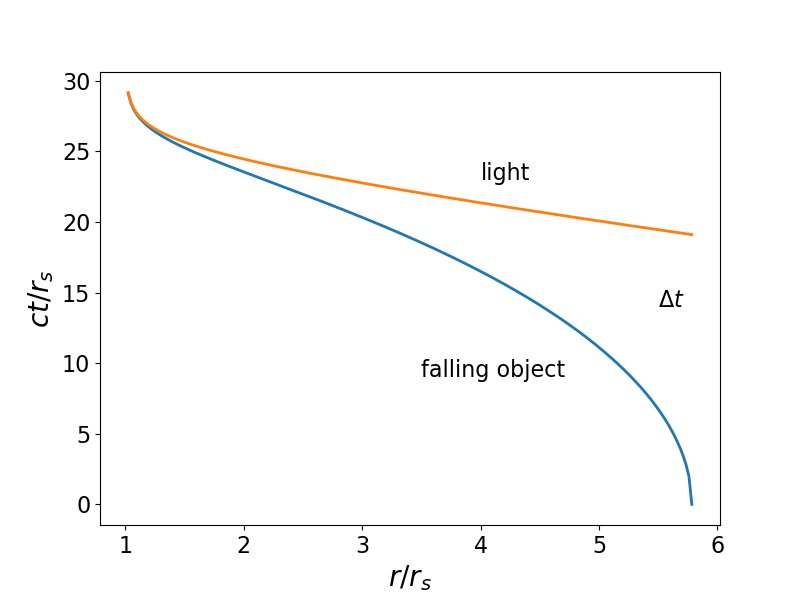
Un exemple du cas limite est présenté ci-dessous. La courbe rouge est la géodésique légère tandis que la courbe bleue montre la géodésique d'un objet tombant de l'infini et passant par (dans ce cas) $ 5.8r_s $ à $ t = 0 $. Seuls les événements sous la courbe rouge pouvaient être vus par un observateur en baisse.

J'ai ensuite "dérivé" cette courbe de manière analytique. Réorganiser l'équation (1) que nous pouvons écrire $$ r - r_s = (r_0-r_s) \ exp ((a + \ Delta t -r) / r_s) \ exp (-t / r_s) $$ et si (proche de la limite où il est possible pour la lumière d'intercepter l'objet tombant) on laisse $ t $ devenir grand, alors $ r \ rightarrow r_s $ et on peut écrire $$ r - r_s \ simeq (r_0 - r_s) \ exp ((a + \ Delta t -r_s) / r_s) \ exp (-t / r_s) \,, \ tag {4} $$ où nous exploitons le fait que la limite de $ r \ exp (-r / r_s) $ comme $ r \ rightarrow r_s $ est juste $ r / e $.

En réorganisant l'équation (2) de la même manière, on obtient $$ \ frac {\ sqrt {r / r_s} - 1} {\ sqrt {r / r_s} +1} = \ exp (-t / r_s) \ exp \ left (- \ frac {2} {3} \ gauche (\ frac {r} {r_s} \ droite) ^ {3/2} -2 \ gauche (\ frac {r} {r_s} \ droite) ^ {1/2} + \ frac {b} {r_s} \droite)\, . $$ Encore une fois, nous soutenons que autour du cas limite $ r \ rightarrow r_s $ et ainsi nous pouvons écrire $$ \ sqrt {r / r_s} = 1 + 2 \ exp (b / r_s - 8/3) \ exp (-t / r_s) $$ Mettre au carré ceci et négliger le terme $ \ exp (-2t / r_s) $: $$ r - r_s \ simeq 4r_s \ exp (b / r_s - 8/3) \ exp (-t / r_s)) \ tag {5} $$

Il y a ou non un point d'interception est déterminé par le fait que le rapport des équations (4) et (5) est inférieur à 1 comme $ t \ rightarrow \ infty $. $$ \ lim_ {t \ rightarrow \ infty} \ frac {(r_0 - r_s) \ exp ((a + \ Delta t -r_s) / r_s) \ exp (-t / r_s)} {r_s (1 + 4 \ exp (b / r_s - 8/3) \ exp (-t / r_s))} < 1 \, $$ qui conduit à $$ \ frac {(r_0 - r_s) \ exp ((a + \ Delta t -r_s) / r_s)} {4r_s \ exp (b / r_s - 8/3)} < 1 $$ $$ \ exp (\ Delta t / r_s) < \ frac {4r_s} {r_0 - r_s} \ exp (\ frac {b - a} {r_s} - \ frac {5} {3}) $$ $$ \ Delta t < \ ln \ left (\ frac {4r_s} {r_0 - r_s} \ right) r_s + \ left (\ frac {b - a} {r_s} - \ frac {5} {3} \ right ) r_s $$ Réinsertion des expressions pour $ a $ et $ b $ $$ \ Delta t < \ ln \ left (\ frac {4r_s} {r_0 - r_s} \ right) r_s + \ left (\ frac {2} {3} \ left (\ frac {r_0} {r_s} \ right) ) ^ {3/2} + 2 \ gauche (\ frac {r_0} {r_s} \ droite) ^ {1/2} - \ ln \ gauche | \ frac {\ sqrt {r_0 / r_s} + 1} {\ sqrt {r_0 / r_s} -1} \ right | - \ frac {5} {3} \ right) r_s - r_0 $$ Cela correspond à ce qui est tracé ci-dessus.

Pour transformer cela en un intervalle de temps maximum propre $ \ Delta \ tau $ du point de vue de l'observateur, le résultat serait multiplié par $ (1 - r_s / r_0) ^ {1/2} $.

(b) Objet tombant du repos à $ t_0, r_0 $

Maintenant, la configuration est que l'observateur libère l'objet de $ t_0, r_0 $, puis attend un intervalle de temps (coordonné) $ \ Delta t $ avant de signaler.

L'équation (1) est toujours valide dans ce scénario, cependant l'équation (2) doit être remplacée par la géodésique suivante pour un objet tombant librement du repos à $ t_0, r_0 $. $$ \ frac {t-t_0} {r_s} = \ ln \ left | \ frac {(r_0 / r_s -1) ^ {1/2} + \ tan (\ eta / 2)} {(r_0 / r_s -1) ^ {1/2} - \ tan (\ eta / 2)} \ right | + \ left (\ frac {r_0} {r_s} -1 \ right) ^ {1/2} \ left (\ eta + \ frac {r_0} {2r_s} (\ eta + \ sin \ eta) \ right). \ tag {6} $$ Ici le "paramètre cycloïde" $ \ eta (r) $ est défini par $$ r = \ frac {r_0} {2} (1 + \ cos \ eta) $$

Comme $ r \ rightarrow r_s $, le premier terme de l'équation (6) croît de façon exponentielle tandis que le deuxième terme, que je définirai comme $ b (r) / r_s $, tend vers une constante: $$ \ lim_ {r \ rightarrow r_s} b (r) = b _ {\ rm rs} = r_s \ left (\ frac {r_0} {r_s} -1 \ right) ^ {1/2} \ left (\ eta_ {\ rm rs} + \ frac {r_0} {2r_s} (\ eta _ {\ rm rs} + \ sin \ eta _ {\ rm rs}) \ right), $$ où $$ \ cos \ eta _ {\ rm rs} = \ gauche (\ frac {2r_s} {r_0} -1 \ droite). $$

En utilisant l'identité que $ \ tan \ eta / 2 = \ sin \ eta / (1 + \ cos \ eta) $, alors $$ \ tan (\ eta / 2) = \ gauche (\ frac {r_0} {r} - 1 \ droite) ^ {1/2}. $$ En remplaçant cela dans l'équation (6), nous pouvons définir $ t_0 = 0 $, exponentiellement et trouver $$ \ left (\ frac {r_0} {r_s} -1 \ right) ^ {1/2} \ left (1 - \ exp \ left [\ frac {bt} {r_s} \ right] \ right) = \ left (\ frac {r_0} {r} -1 \ right) ^ {1/2} \ left (1 + \ exp \ left [\ frac {bt} {r_s} \ right] \ right) $$ En mettant cela au carré et en négligeant les termes contenant $ \ exp (-2t / r_s) $ lorsque $ t $ devient grand, cela peut être réorganisé pour donner $$ r = r_s \ frac {\ left (1 + 2 \ exp [(bt) / r_s] \ right)} {1 - 2 \ exp [(bt) / r_s] + (4r_s / r_0) \ exp [( bt) / r_s]}. $$ Encore une fois, comme nous recherchons un comportement limitant à grand $ t $, alors le dénominateur peut être développé comme un binôme, en ne conservant que les deux premiers termes. La multiplication avec le numérateur donne alors: $$ r -r_s \ simeq 4r_s \ left (1 - \ frac {r_s} {r_0} \ right) \ exp \ left [\ frac {b-t} {r_s} \ right]. \ tag {7} $$

Pour trouver la limite $ \ Delta t $ pour laquelle un faisceau lumineux de l'observateur "attrapera" l'objet qui tombe, nous prenons le rapport des équations 4 et 7, posons $ b = b _ {\ rm rs} $ et exiger que ce soit inférieur à 1. Cela donne $$ \ exp \ left [\ frac {\ Delta t} {r_s} \ right] < 4 \ left (\ frac {r_s} {r_0} \ right) \ exp \ left [\ frac {b _ {\ rm rs} } {r_s} \ right] \ exp \ left [\ frac {r_s-r_0} {r_s} \ right] $$ et donc $$ \ Delta t < r_s \ ln \ left (\ frac {4r_s} {r_0} \ right) + b _ {\ rm rs} + r_s - r_0 $$

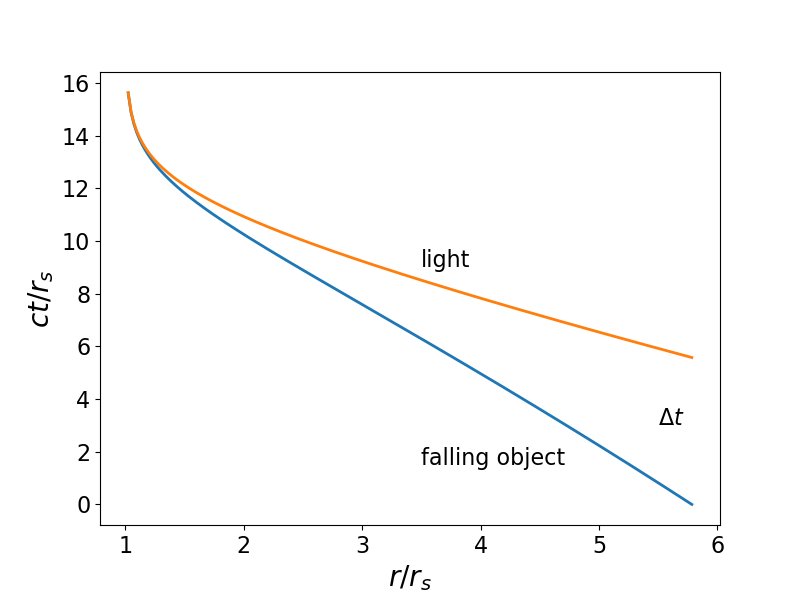
Le résultat est tracé ci-dessous comme la courbe rouge (et j'ai confirmé qu'il est correct en utilisant une méthode de bissection numérique) et comparé au cas 1 avec l'objet en chute libre de l'infini (courbe bleue, comme dans la première image). Comme prévu, le $ \ Delta t $ autorisé est plus grand lorsque l'objet est libéré du repos.

Comme précédemment, ce résultat est l'intervalle de temps maximal des coordonnées Schwarzschild. Il doit être réduit du facteur de dilatation du temps approprié $ (1-r_s / r_0) ^ {1/2} $ pour donner l'intervalle de temps approprié maximum.

Un exemple du cas limite est présenté ci-dessous. La courbe rouge est la géodésique de la lumière, la courbe bleue est la géodésique de l'objet qui tombe. Seuls les événements sous la courbe rouge (qui asymptote à un gradient de -1) peuvent être "vus" par un objet tombant dans un trou noir depuis le repos, à partir (dans ce cas) d'environ 5,8r_s $.

2. Si la lumière peut intercepter un objet avant qu'il n'atteigne la singularité

La réponse ci-dessus donne le délai maximum (coordonné) pour qu'un signal d'un observateur stationnaire atteigne un objet tombant avant qu'il n'atteigne l'horizon des événements, $ (\ Delta t) _ {\ rm EH} $. Mais cela ne répond pas complètement à la question (du titre), car l'objet peut encore recevoir de la lumière pendant le temps qu'il faut pour atteindre la singularité après traverser l'horizon des événements. Cela se voit le plus clairement dans les coordonnées de Kruskal-Szekeres, mais encore une fois, il est possible de résoudre ce problème (assez facilement) en coordonnées de Schwarzschild.

La condition ici est que le temps de coordonnées de la géodésique de lumière retardée doit être inférieur ou égal au temps de coordonnées de la géodésique de l'objet tombant à $ r = 0 $.

Cette condition est en fait assez facile à trouver. Pour le cas de l'objet tombant librement de l'infini, les équations (1-3) montrent que le $ \ Delta t $ original que j'ai dérivé doit être augmenté comme $$ (\ Delta t) _ {\ rm singularité} = r_s \ ln \ left (\ frac {r_s} {r_0-r_s} \ right) - r_s \ left (- \ frac {2} {3} \ left ( \ frac {r_0} {r_s} \ right) ^ {3/2} - 2 \ left (\ frac {r_0} {r_s} \ right) ^ {1/2} + \ ln \ left | \ frac {\ sqrt {r_0 / r_s} + 1} {\ sqrt {r_0 / r_s} -1} \ right | \ right) - r_0 $$ Ou en termes de résultat précédent. 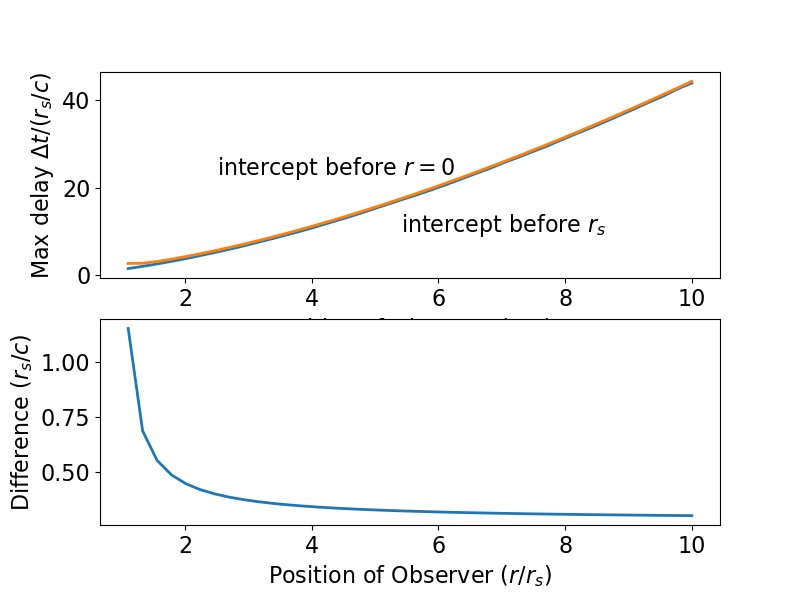$$ (\ Delta t) _ {\ rm singularité} = (\ Delta t) _ {\ rm EH} + r_s \ left (\ frac {5} {3} - 2 \ ln 2 \ right) = (\ Delta t) _ {\ rm EH} + 0,280r_s $$

Pour le cas d'un objet tombant du repos, on voit que $ \ eta = \ pi $ at $ r = 0 $, de sorte que si le temps de coordonnée est inférieur ou égal au temps de coordonnée de l'objet à $ r = 0 $ est obtenu à partir des équations (1) et (6) comme $$ (\ Delta t) _ {\ rm singularité} = r_s \ ln \ left (\ frac {r_s} {r_0-r_s} \ right) + \ pi r_s \ left (\ frac {r_0} {r_s} -1 \ droite) ^ {1/2} \ gauche (1 + \ frac {r_0} {2r_s} \ droite) -r_0, $$ qui est plus grand que $ (\ Delta t) _ {\ rm EH} $ d'un montant qui dépend de $ r_0 $, mais qui est asymptotique à la baisse des résultats de l'infini lorsque $ r_0 $ devient grand. 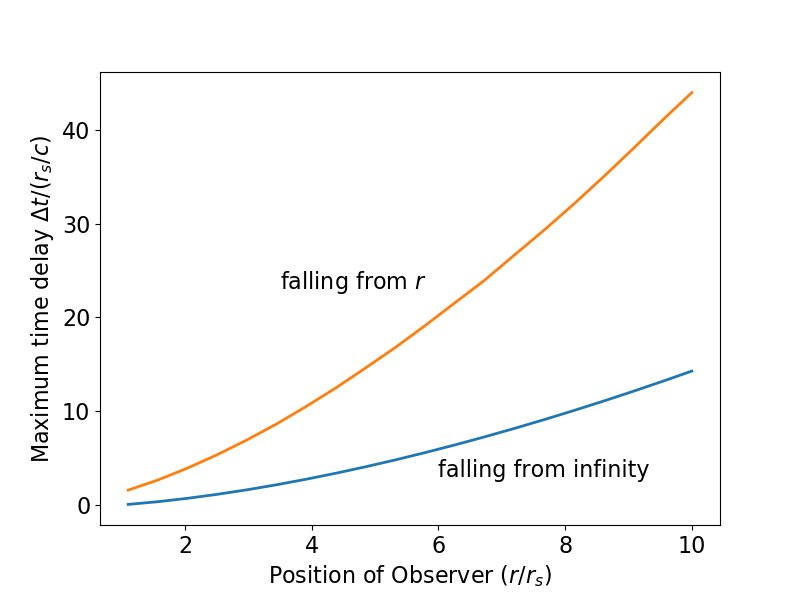Cette nouvelle relation est tracée ci-dessous - la courbe rouge supérieure est le retard maximum (temps de coordonnées) qui peut être toléré et envoyer toujours un signal qui atteint l'objet qui tombe avant la singularité.Le graphique inférieur montre la différence entre ce résultat et le résultat précédent pour que le retard atteigne toujours l'objet avant l'horizon des événements.

Le graphique ci-dessous devrait rendre les choses plus claires.Il montre les géodésiques de chaque côté ou $ r_s $ dans le cas d'un objet tombant de $ r = 2r_s $ à $ t = 0 $.La géodésique légère en rouge est celle calculée de sorte qu'elle intercepte juste l'objet comme $ r \ rightarrow r_ {s} $ et a $ (\ Delta t) _ {\ rm EH} = 3,834 r_s / c $.Mais on voit que cette géodésique "dépasse" l'objet qui tombe avant qu'il n'atteigne la singularité à $ r = 0 $.Cependant, la géodésique de la lumière verte, avec $ (\ Delta t) _ {\ rm singularité} = 4.283 r_s / c $ intercepte l'objet géodésique exactement à $ r = 0 $.

Inspiré par une question similaire, j'ai travaillé sur ce sujet en même temps que Rob Jeffries. Irritant, il m'a battu dessus; mais comme j'utilise une approche légèrement différente et que je ne veux pas que mes efforts soient vains, je posterai ma propre dérivation. Si rien d'autre, cela sert de confirmation de sa réponse fantastique :)

Commençons par indiquer les coordonnées (région I) Kruskal – Szekeres

$$ u = f (r) \ cosh \ left (\ frac {ct} {2r_ \ text {s}} \ right), \ qquad v = f (r) \ sinh \ left (\ frac {ct } {2r_ \ text {s}} \ right), \\ f (r) = \ left (\ frac {r} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2} \, \ text {e} ^ {r / 2r_ \ text {s }}. $$

Comme on le sait, dans ces coordonnées, les géodésiques des rayons lumineux infaillant radialement sont des lignes droites à des angles $ -45 ^ \ circ $. En effet, si on branche $ u + v = k $ dans les équations, avec $ k $ une constante, alors à partir de $ u ^ 2 - v ^ 2 = f (r) ^ 2 $ on trouve $ k (u -v) = f (r) ^ 2 $, de sorte que $$ k \ exp \ left (- \ frac {ct} {2r_ \ text {s}} \ right) = f (r) = \ left (\ frac {r} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2} \, \ exp \ left (\ frac {r} {2r_ \ text {s}} \ right), $$ ou $$ \ frac {ct} {r_ \ text {s}} = \ ln (k ^ 2) - \ frac {r} {r_ \ text {s}} - \ ln \ left (\ frac {r} {r_ \ text {s}} - 1 \ droite), $$ qui sont en effet les géodésiques d'un photon infaillant radialement, avec $ k = f (r_ {0, \ gamma}) $ et $ r_ {0, \ gamma} $ la position initiale du photon à $ t = 0 $.

Maintenant, supposons que nous ayons un objet infaillant radialement, qui commence au repos à une position $ r_0 $ à $ t = 0 $. Quels photons infaillés radialement atteindront l'objet avant qu'il ne traverse l'horizon des événements? Pour répondre à cela, nous allons essayer de dériver la géodésique d'un photon infaillant radialement de telle sorte qu'il rattrape l'objet juste à l'horizon des événements.

La géodésique d'un objet infaillant radialement peut être écrite sous la forme (Misner, Thorne & Wheeler Eq. (31.10), Pag. 824) $$ \ begin {align} r & = \ frac {r_0} {2} (1+ \ cos \ eta) = r_0 \ cos ^ 2 \ eta / 2, \\ \ frac {c \ tau} {r_ \ text {s}} & = \ frac {1} {2} \ left (\ frac {r_0} {r_ \ text {s}} \ right) ^ {\! 3 / 2} (\ eta + \ sin \ eta), \\ \ frac {ct} {r_ \ text {s}} & = \ ln \ left (\ frac {\ sqrt {r_0 / r_ \ text {s} -1} + \ tan \ eta / 2} {\ sqrt {r_0 / r_ \ text {s} -1} - \ tan \ eta / 2} \ right) + \ left (\ frac {r_0} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2 } \ left (\ eta + \ frac {r_0} {2r_ \ text {s}} (\ eta + \ sin \ eta) \ right). \ end {align} $$ Il est également instructif d'introduire l'énergie totale (sans dimension) de l'objet $$ E = \ frac {\ mathcal {E}} {mc ^ 2} = \ left (1- \ frac {r_ \ text {s}} {r} \ right) \ frac {\ text {d} t} {\ texte {d} \ tau}. $$ Les orbites radiales satisfont l'équation $$ \ left (\ frac {\ text {d} r} {c \, \ text {d} \ tau} \ right) ^ 2 = E ^ 2 - \ left (1- \ frac {r_ \ text {s}} {r} \ droite), $$ donc si l'objet est au repos à la position $ r_0 $ à $ t = \ tau = 0 $, alors $$ E = \ sqrt {1- \ frac {r_ \ text {s}} {r_0}}. $$ L'équation pour $ t (\ eta) $ peut donc être réécrite comme $$ \ frac {ct} {r_ \ text {s}} = \ ln \ left (\ frac {E + \ sqrt {1-E ^ 2} \ tan \ eta / 2} {E - \ sqrt {1-E ^ 2} \ tan \ eta / 2} \ right) + \ frac {E} {\ sqrt {1-E ^ 2}} \ left (\ eta + \ frac {\ eta + \ sin \ eta} {2 (1 -E ^ 2)} \ droite). $$ Ensuite, je suivrai cet article (qui contient quelques erreurs) pour déterminer comment cette équation se comporte lorsque $ r $ s'approche de l'horizon des événements. Nous écrivons $$ r = r_ \ text {s} (1+ \ varepsilon), \ qquad \ varepsilon \ rightarrow 0. $$ Près de l'horizon des événements, nous pouvons ignorer les termes d'ordre supérieur dans $ \ varepsilon $, de sorte que $$ \ begin {align} \ cos ^ 2 \ eta / 2 & = (1+ \ varepsilon) \ frac {r_ \ text {s}} {r_0} = (1+ \ varepsilon) (1-E ^ 2) = 1 - E ^ 2 + \ varepsilon (1-E ^ 2), \\ \ sin ^ 2 \ eta / 2 & = E ^ 2 - \ varepsilon (1-E ^ 2), \ end {align} $$ et $$ \ begin {align} (1-E ^ 2) \ tan ^ 2 \ eta / 2 & = \ frac {E ^ 2 - \ varepsilon (1-E ^ 2)} {(1+ \ varepsilon)} \\ & \ approx \ left [ E ^ 2 - \ varepsilon (1-E ^ 2) \ right] (1- \ varepsilon) \\ & \ approx E ^ 2 - \ varepsilon (1-E ^ 2) - \ varepsilon) E ^ 2 = E ^ 2 - \ varepsilon. \ end {align} $$ Par conséquent, $$ \ begin {align} E + \ sqrt {1-E ^ 2} \ tan \ eta / 2& \ approx E \ left (1 + \ sqrt {1 - \ varepsilon / E ^ 2} \ right) \\ & \ approx 2E - \ frac {\ varepsilon} {2E} \ approx 2E, \ end {align} $$ et $$ \ begin {align} E - \ sqrt {1-E ^ 2} \ tan \ eta / 2& \ approx E \ left (1 - \ sqrt {1 - \ varepsilon / E ^ 2} \ right) \\ & \ approx \ frac {\ varepsilon} {2E}, \ end {align} $$ Pour que finalement, comme $ r \ rightarrow r_ \ text {s} $, $$ \ frac {ct_ \ text {s}} {r_ \ text {s}} \ approx \ ln \ left (\ frac {4E ^ 2} {\ varepsilon} \ right) + \ frac {E} {\ sqrt {1 -E ^ 2}} \ left (\ eta_ \ text {s} + \ frac {\ eta_ \ text {s} + \ sin \ eta_ \ text {s}} {2 (1-E ^ 2)} \ right ), $$ avec $ \ eta_ \ text {s} $ la valeur de $ \ eta $ à l'horizon des événements. Depuis $ \ cosh (x) = \ sinh (x) \ rightarrow \ text {e} ^ x / 2 $ as $ x \ rightarrow \ infty $, les coordonnées de Kruskal – Szekeres de l'objet à l'horizon des événements deviennent (puisque $ t \ rightarrow \ infty $) $$ \ begin {align} u_ \ text {s} ^ 2 = v_ \ text {s} ^ 2 & = \ frac {1} {4} f (r_ \ text {s}) ^ 2 \, \ exp \ left (\ frac {ct_ \ text {s}} {r_ \ text {s}} \ right) = \ frac {\ varepsilon \ text {e}} {4} \ exp \ left (\ frac {ct_ \ text {s}} {r_ \ text {s}} \ right) \\ & = \ text {e} E ^ 2 \ exp \ left [\ frac {E} {\ sqrt {1-E ^ 2}} \ left (\ eta_ \ text {s} + \ frac {\ eta_ \ text {s} + \ sin \ eta_ \ text { s}} {2 (1-E ^ 2)} \ right) \ right], \ end {align} $$ ou $$ \ begin {align} u_ \ text {s} = v_ \ text {s} & = \ sqrt {\ text {e}} E \ exp \ left [\ frac {E} {2 \ sqrt {1-E ^ 2}} \ left (\ eta_ \ text {s} + \ frac {\ eta_ \ text {s} + \ sin \ eta_ \ text {s}} {2 (1-E ^ 2)} \ right) \ right] \\ & = \ sqrt {\ text {e}} \ sqrt {\ frac {r_ \ text {s}} {r_0}} \ left (\ frac {r_0} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2} \ exp \ left [\ frac {1} {2} \ left (\ frac {r_0} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2} \ left (\ eta_ \ text { s} + \ frac {r_0} {2r_ \ text {s}} (\ eta_ \ text {s} + \ sin \ eta_ \ text {s}) \ right) \ right]. \ end {align} $$ Les coordonnées correspondantes pour un photon infaillant radialement satisfont $ u_ \ text {s} + v_ \ text {s} = k_ \ text {b} $, pour une valeur limite $ k_ \ text {b} $. Donc $ k_ \ text {b} = 2u_ \ text {s} $ et nous trouvons la géodésique nulle correspondante $$ \ frac {ct} {r_ \ text {s}} = \ ln (k_ \ text {b} ^ 2) - \ frac {r} {r_ \ text {s}} - \ ln \ left (\ frac {r } {r_ \ text {s}} - 1 \ right). $$ Nous pourrions résoudre cela pour $ r $ à $ t = 0 $, ce qui donne un rayon de frontière $ r_ \ text {b} $ au-delà duquel les photons infaillés radialement ne peuvent pas rattraper l'objet avant qu'il ne traverse l'horizon des événements. Alternativement, nous pourrions brancher $ r = r_0 $ et demander quel est le temps maximum $ \ Delta t $ tel que les photons envoyés à $ r_0 $ avant $ t = \ Delta t $ puissent encore rattraper l'objet. Nous trouvons $$ \ begin {align} \ frac {c \ Delta t} {r_ \ text {s}} & = \ ln (k_ \ text {b} ^ 2) - \ frac {r_0} {r_ \ text {s}} - \ ln \ left ( \ frac {r_0} {r_ \ text {s}} - 1 \ right) \\ & = 1 + \ ln \ left (\ frac {4r_ \ text {s}} {r_0} \ right) + \ left [\ left (\ frac {r_0} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2} \ left (\ eta_ \ text {s} + \ frac {r_0} {2r_ \ text {s}} (\ eta_ \ text {s} + \ sin \ eta_ \ text {s} ) \ right) \ right] - \ frac {r_0} {r_ \ text {s}}, \ end {align} $$ qui est exactement le même résultat que celui donné par Rob Jeffries.

J'ai fait un tracé pour visualiser les résultats, en coordonnées Schwarzschild et Kruskal – Szekeres:

La courbe bleue est la géodésique d'un objet, au repos à $ t = 0 $ (ici, $ r_0 = 2r_ \ text {s} $). La courbe orange est la géodésique d'un photon qui est à la position $ r_0 $ à $ t = 0 $. La courbe rouge est la géodésique que j'ai dérivée dans cet article. Il commence à la position $ r_ \ text {b} $ à $ t = 0 $ et rattrape l'objet juste à l'horizon des événements. Les géodésiques des photons qui se trouvent entre les courbes orange et rouge (j'en ai tracé deux, les courbes en pointillés) rattraperont l'objet, les géodésiques au-delà de la courbe rouge ne le seront pas.

Pour compléter les excellentes réponses ci-dessus, voici un diagramme de l'espace-temps en coordonnées Gullstrand-Painleve ou "pluie".Ceci est tiré du superbe et accessible livre Exploring Black Holes (2000) de Taylor & Wheeler, $ \ S B.6 $.Leur métaphore «pluie» signifie une particule d'essai avec une masse, qui est initialement tombée du repos loin du trou noir.Considérez-les comme des astronautes / observateurs, pour ce problème.

$ t_ \ textrm {rain} $ est l'heure propre d'une goutte de pluie, qui est utilisée comme coordonnée.$ r $ est la coordonnée de courbure habituelle comme dans les coordonnées Schwarzschild [-Droste], et $ M $ est la masse du trou noir.Le diagramme montre que la plupart des "impulsions lumineuses" ne rattrapent jamais un "plongeur de pluie" donné;en particulier, ils ne verront pas la fin de l'univers.

Non. Le trou noir s'évaporera complètement en un temps fini, donc à la fin de l'univers, il n'existera plus.

Votre question est due à une certaine confusion avec le concept d'espace-temps d'un trou noir. Vous devez faire la distinction entre votre système de coordonnées et ce que vous voyez. Les deux sont des concepts différents: Un exemple simple est un espace de Minkowski: si un diagramme de Minkowski représente vos coordonnées, vous obtenez une vue en quatre dimensions de tout l'espace-temps. En revanche, ce que vous voyez, ce sont des éléments qui se trouvent sur votre lightcone qui montre dans le passé.

Près d'un trou noir, nous devons appliquer la même distinction de ce double concept qui peut être montré dans le diagramme de Kruskal suivant, avec une particule infaillante A et une particule restant à l'extérieur de B:

Les coordonnées temporelles d'un observateur lointain sont indiquées par les lignes passant par le centre: t = 0, t = 1, t = 2, limité par l'horizon des événements où t = $ \ infty $. Selon ces coordonnées temporelles, la particule infaillante n'atteindra jamais l'horizon. Et inversement, lorsque A s'approche de l'horizon, l'horloge d'un observateur extérieur se rapprochera de la fin des temps.

C'est peut-être la raison pour laquelle vous avez posé votre question. Mais votre question ne demande pas: quelle est la position par rapport aux coordonnées d'un observateur extérieur, mais: que voit la particule infaillante, et pour cette question vous devez vous référer (comme indiqué dans d'autres réponses) au petit 45 ° - flèches entre les particules communicantes A et B. Les 3 flèches diagonales du bas vers la gauche indiquent que B est à un certain point lorsque A touche l'horizon des événements.