Que veulent dire les physiciens par temps?

Nous allons commencer par la simple question qu'est-ce que les physiciens entendent par temps .

Notez que c'est facilese confondre entre les notions de temps et l'écoulement du temps .Lorsque les non-physiciens parlent du temps, ils signifient généralement l'écoulement du temps, c'est-à-dire le fait que dans l'expérience humaine, le temps s'écoule inexorablement (à une seconde par seconde).Nous y reviendrons, mais pour l'instant, nous ignorerons la question de savoir pourquoi le temps s'écoule et aborderons simplement ce que le temps signifie pour un physicien.

Si vous voulez localiser une position dans l'espace, une méthode estpour configurer certains axes, par exemple $ x $ , $ y $ et $ z $ span>, et vous pouvez alors identifier de manière unique tout point dans l'espace par ses coordonnées $ (x, y, z) $ .

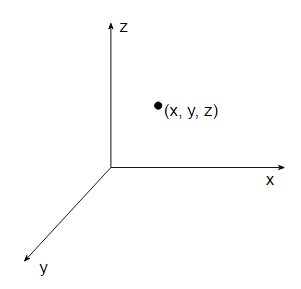
Pour faire la distinction entre les événements se produisant au même endroit dans l'espace mais à des moments différents, nous devons spécifier quand un événement s'est produit ainsi que où il s'est produit, nous ajoutons donc une coordonnée temporelle $ t $ . Les événements peuvent alors être localisés de manière unique par leurs coordonnées espace-temps $ (t, x, y, z) $ . Pour un physicien, le temps n'est qu'une coordonnée utilisée pour spécifier des événements dans l'espace-temps. Dans la figure 1 ci-dessus, nous avons un axe $ x $ s'étendant de $ - \ infty $ à $ \ infty $ , un axe $ y $ s'étendant depuis $ - \ infty $ à $ \ infty $ et un axe $ z $ s'étendant à partir de $ - \ infty $ à $ \ infty $ . À ceux-ci, un physicien ajoute un axe $ t $ s'étendant de $ - \ infty $ à $ \ infty $ , et c'est ce que l'heure est - juste une coordonnée.

Mais l'expérience quotidienne nous dit que le temps est spécial - certainement différent de l'espace - alors ce qui justifie l'opinion du physicien selon laquelle le temps n'est qu'une coordonnée? Pour comprendre cela, commencez par le temps dans le monde quotidien tel que décrit par la mécanique newtonienne.

Supposons que je mette en place un système de coordonnées avec moi-même à l'origine, $ x $ à l'est, $ y $ au nord et $ z $ vers le haut. Pendant le temps, j'utiliserai ma montre-bracelet. Et supposons que vous fassiez de même, mais disons que vous êtes dans un pays différent de moi. Nos deux ensembles de coordonnées ne correspondent pas, car nos axes est, nord et haut pointent dans des directions différentes.

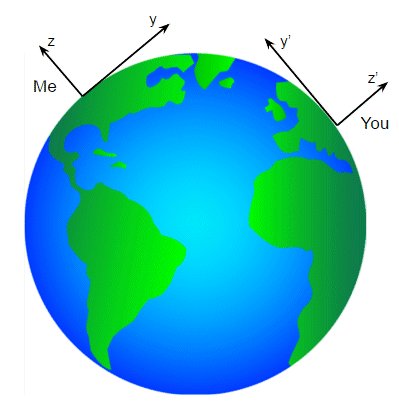
Ou supposons que vous vous déplaciez par rapport à moi. Même en ignorant la courbure de la surface de la Terre, nos coordonnées ne correspondent pas car votre origine se déplace constamment par rapport à mon origine - ce qui semble être stationnaire pour moi se déplace dans vos coordonnées et vice versa .

Les coordonnées spatiales dépendent donc de l'observateur. Cependant, le temps est absolu. En supposant que nous utilisons tous les deux le Greenwich Mean Tim e (ou une autre norme similaire), nous serons toujours d'accord sur l'heure, peu importe où nous sommes sur Terre ou comment nous nous déplaçons l'un par rapport à l'autre. En mécanique newtonienne, le temps est spécial pour cette raison, il est donc logique de le considérer séparément de l'espace.

Cependant, depuis 1905, nous savons que pour décrire correctement le monde qui nous entoure, nous devons utiliser la relativité restreinte, et en relativité, le temps n'est pas le même pour tous les observateurs. Revenons un instant à la mécanique newtonienne ordinaire et supposons que vous vous déplaciez par rapport à moi le long de l'axe $ x $ à une certaine vitesse $ v $ . Si nous dessinons mes axes de temps $ t $ et de position $ x $ et vos $ t '$ et $ x' $ axes auxquels ils ressembleraient:

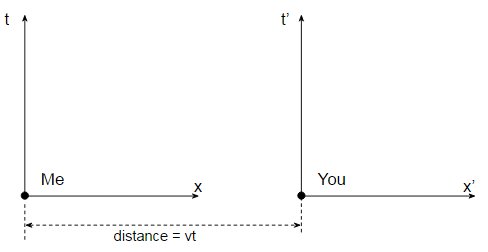
Nos deux axes temporels pointent dans la même direction, donc nous sommes tous les deux d'accord sur ce que signifie définir un axe temporel. Mais maintenant, supposons que vous vous déplaciez à une vitesse relativiste $ v $ et que vous dessiniez le même diagramme.

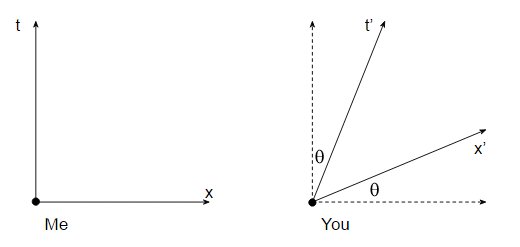
Lorsque nous incluons la relativité restreinte, nos axes ne pointent plus dans la même direction. Si je trace mon axe des temps vers le haut, alors par rapport à moi, votre axe des temps est tourné d'un angle $ \ theta $ donné par:

$$ \ tan (\ theta) = \ frac {v} {c} $$

Votre direction temporelle est donc un mélange de mes directions temporelles et spatiales . Vous verriez exactement la même chose: si vous dessinez votre axe du temps vers le haut, vous verriez mon axe du temps tourné de $ - \ theta $ . En effet, nous avons différentes définitions du temps, et c'est pourquoi nous obtenons une dilatation du temps en relativité.

Le point de tout cela est qu'en relativité, le temps n'est pas défini de manière unique. Lorsque nous considérons les coordonnées utilisées par différents observateurs, nous constatons que le temps et l'espace se mélangent. Le temps n'est plus distinct de l'espace, et c'est pourquoi les physiciens le traitent comme l'une des quatre coordonnées qui forment ensemble l'espace-temps à quatre dimensions.

Comment le temps s'écoule-t-il?

Le précédent section expliquait ce que les physiciens entendaient par temps, mais ne mentionnait pas le temps qui s'écoule. En effet, en relativité, le temps ne s'écoule pas - plus précisément le flux du temps n'existe pas en tant que concept.

Cela va demander quelques explications, alors laissez-moi essayez-le en utilisant un exemple simple. Supposons que je vous lance une balle et que vous l'attrapiez. L'expérience de tous les jours nous dit que le temps s'écoule vers l'avant et, ce faisant, la balle monte de ma main puis tombe dans votre main. Si nous représentons la hauteur de la balle, $ h $ , en fonction du temps, $ t $ , nous ' J'obtiendrai quelque chose comme:

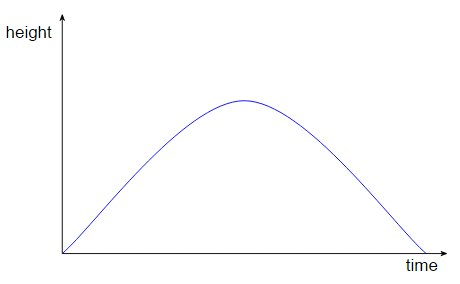
En physique newtonienne, cela a une belle interprétation simple: le temps s'écoule en avant et la hauteur est fonction du temps . Nous pouvons écrire la hauteur sous la forme $ h (t) $ . Mais maintenant, permettez-moi de dessiner un graphique différent. Je vais représenter graphiquement la hauteur de la balle, $ h $ , par rapport à la distance, $ d $ , la balle se déplace horizontalement en passant de moi à vous:

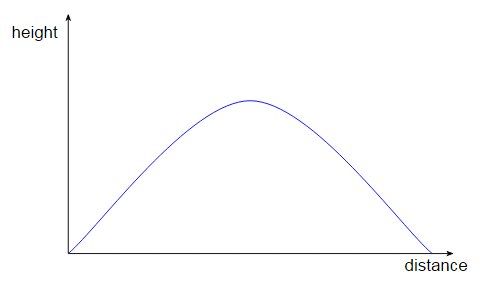
Cela ressemble terriblement au graphique précédent, et en effet je peux écrire la hauteur de la balle en fonction de la distance horizontale parcourue, $ h (d) $ . Mais nous ne dirions pas que la distance $ d $ avance et que la hauteur change en même temps, car, eh bien, le temps est différent de la distance. Les deux graphiques ne sont que des vues différentes d'un graphique à quatre dimensions montrant la trajectoire de la balle dans l'espace-temps (je ne vais dessiner que trois dimensions car je ne peux pas faire de graphiques 4D):

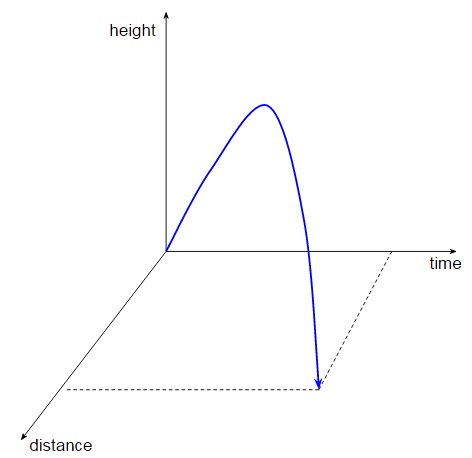
Dans la section précédente, je me suis donné quelques longueurs pour expliquer que le temps n'est qu'une coordonnée, comme les coordonnées spatiales, donc ce graphique n'est pas montrer que le temps s'écoule, pas plus que la distance ou la hauteur s'écoulent. La trajectoire de la balle n'est qu'une ligne dans un 4D.

En relativité, nous appelons des graphes comme les lignes du monde ci-dessus, où la ligne du monde n'est que l'ensemble de tous les points de l'espace-temps $ (t, x, y, z) $ que la balle occupe pendant sa trajectoire. Cette ligne du monde est un objet fixe dans un espace-temps à quatre dimensions - elle ne change pas avec le temps. Tout ce qui change, c’est la position de la balle sur la ligne du monde. C’est pourquoi nous disons que le temps ne passe pas. Le temps n'est qu'une des quatre dimensions qu'occupe la ligne du monde.

En fait, toute propriété physique, pression d'un gaz, force d'un champ gravitationnel, ou autre, peut être écrite comme une fonction dans les quatre dimensions de l'espace-temps, $ F (t, x, y, z) $ . Écrit de cette façon, l’objet géométrique $ F $ existe dans tout l’espace et tout le temps - ce n’est pas plus quelque chose qui évolue dans le temps que quelque chose qui évolue dans l’espace. En principe, nous pourrions avoir une fonction qui représentait l'univers entier, $ \ mathcal {F} (t, x, y, z) $ , et cela existerait pour tous valeurs de $ t $ , $ x $ , $ y $ et $ z $ . Cette idée (ou une gamme d’idées similaires) s’appelle l’univers de blocs - l’idée que l’univers entier existe simultanément et que le temps ne coule pas.

À ce stade, je Il convient de noter que de nombreux physiciens, et je suppose que la grande majorité des non-physiciens, diraient que ce n'est que de la sottise mathématique et qu'il est absurde de dire que le temps ne s'écoule pas. Je ne vais pas faire de commentaire, sauf pour dire que cela nous amène bien à la dernière de nos questions.

Pourquoi y a-t-il une flèche de temps?

Cependant mathématiquement convaincant l'idée d'un univers bloc peut être, il n'en reste pas moins que notre expérience quotidienne nous dit que:

1. le temps s'écoule

2. it flux dans une direction - vers l'avant et jamais vers l'arrière

Alors, comment concilier cela avec l'idée d'un univers bloc? De nombreux physiciens ont longuement réfléchi à ce sujet, et il existe de nombreux points de vue différents. Cependant, il existe un consensus sur le fait que cela est lié à l ' entropie. En effet, cela est encapsulé dans la deuxième loi de la thermodynamique, qui déclare grosso modo que pour tout système isolé, l'entropie ne fait qu'augmenter.

Pensez à un mécanisme. Nous ne nous soucierons pas exactement de ce que c'est, par exemple, cela pourrait être quelque chose de mécanique, un nuage de gaz interstellaire ou un cerveau humain. Lorsque nous parlons du temps qui s'écoule, nous voulons dire que l'état de la machine change dans une direction spécifique, par ex. une horloge avance, et la deuxième loi de la thermodynamique nous dit qu'elle change dans le sens de l'augmentation de l'entropie.

En supposant que le cerveau humain n'est qu'un mécanisme, il change dans le sens de l'entropie croissante comme tout autre mécanisme. Mais si la conscience est le résultat du changement du cerveau, il s'ensuit que tout être conscient observera des mécanismes changeant dans le sens d'une entropie croissante. Ce n’est pas tant une loi physique qu’une corrélation. Puisque nos cerveaux changent dans la même direction (d'entropie croissante) que tout le reste, cela signifie qu'ils observeront nécessairement que tout change dans cette même direction. Nous appelons cette direction le temps croissant.

Si on me laisse une opinion personnelle, je dirais que tout cela semble un peu banal - trop beau pour être vrai - et cela semble une explication étrangement simple pour quelque chose d'aussi compliqué que l'univers. Cependant, je n'ai pas de meilleure suggestion à faire. En effet, je ne pense pas que quiconque ait une meilleure suggestion, ou du moins pas une assez meilleure pour convaincre de larges pans de la communauté des physiciens.

Qu'est-ce que le temps?

Comme l'a dit Einstein, le temps est ce que les horloges mesurent . Et si vous regardez ce que fait réellement une horloge, si vous ouvrez une horloge et jetez un regard scientifique froid sur les preuves empiriques, vous verrez des rouages ​​tourner ou un cristal osciller. Vous verrez que l'horloge comporte une sorte de mouvement cyclique régulier avec quelque chose comme des engrenages ou un dispositif de comptage, et cela donne une sorte d'affichage cumulatif de ce que nous appelons "l'heure". Cependant, tout ce qui s'est réellement passé, c'est que les rouages, etc., ont bougé , et la grande main a bougé avec la petite main. Une fois que vous appréciez cela, la relativité restreinte est simplifiée, en particulier lorsque vous pensez à la nature ondulatoire de la matière. La vitesse maximale de mouvement est la vitesse de la lumière, de sorte que le mouvement macroscopique à travers l'espace entraîne nécessairement une réduction de la vitesse du mouvement local. Consultez la inférence simple de la dilatation du temps sur Wikipedia.

Est-ce que ça coule?

Non, ça ne marche pas. L'eau coule. Vous pouvez le voir couler. Mais lorsque vous essayez de voir le temps s'écouler , tout ce que vous pouvez voir, ce sont des rouages ​​qui tournent ou un cristal oscille. L'idée que le temps s'écoule n'est qu'une figure de style, une abstraction. La lumière se déplace, les planètes bougent, le sang bouge, les signaux électrochimiques bougent, les rouages ​​bougent. Tout bouge et vous pouvez voir cette motion. Mais vous ne pouvez pas voir le temps s'écouler. Parce que non. Une horloge n'est pas un compteur de gaz cosmique qui mesure l'écoulement du temps. Ouvrez un compteur de gaz et vous trouvez du gaz qui y circule. Ouvrez une horloge et vous ne trouverez pas le temps qui passe.

et si oui, qu'est-ce qui définit sa direction?

Il n'y a pas de direction temporelle. C'est aussi une abstraction. Pouvez-vous pointer dans cette direction? Non. Pouvez-vous vous déplacer dans cette direction temporelle? Non. Parce que le temps n'est qu'une mesure cumulative du mouvement, vous ne pouvez pas vous déplacer dans une mesure de mouvement et vous ne pouvez pas prendre de direction.

Que veulent dire les physiciens par temps?

La plupart des physiciens veulent dire la même chose que n'importe qui d'autre.Mais certains vous diront que c'est une coordonnée, qui est une autre chose abstraite, plutôt que quelque chose associé au mouvement ou au changement.

Très bien, je vais moi aussi essayer:

• Que veulent dire les physiciens par temps? Permettez-moi de commencer par une citation d'Hermann Weyl:

Le monde est simplement , cela n’arrive pas . C'est seulement au regard de ma conscience, rampant le long de la ligne de vie de mon corps, qu'une partie de ce monde prend vie comme une image fugace dans l'espace qui change continuellement dans le temps.

Lorsqu'il écrit "Le monde est simplement ", il n'utilise évidemment pas est dans le sens de "existant dans le temps". Le temps (tel que signifié dans la citation) vient à l'existence au moyen de notre conscience (qui divise le monde en un passé et un futur, mais qui en réalité "sont" juste là) qui "rampe" le long de la ligne de vie de notre corps. Une analogie serait un orgue de Barbarie avec un rouleau de musique en papier ponctué. Nous sommes l'orgue de Barbarie (la conscience) et nous nous déplaçons le long du rouleau (le monde qui est simplement), produisant ainsi la musique déjà présente dans son intégralité sur le rouleau. C'est aussi ce que pensait Einstein:

Pour nous, physiciens convaincus, la distinction entre passé, présent et futur n'a d'autre sens que celui d'une illusion, bien que tenace.

Je pense que c'est ainsi que la plupart des physiciens pensent au temps (la naissance, au moyen de notre conscience du mouvement d'un monde qui est simplement; le passé, le présent et le futur coexistent). Mais pour certains, il y en a (ou beaucoup, je n'ai pas enquêté) qui pensent que le temps existe objectivement.

Parce que du même coup, on peut dire que c'est le monde qui change continuellement et non a priori "est simplement". Notre conscience perçoit ce monde en constante évolution comme un monde dans lequel il est temps. Ou, dans l'analogie de l'orgue de Barbarie, nous ne bougeons pas le long du rouleau de musique mais le rouleau de musique se déroule devant nous (sans que toute la musique soit déjà là).

Le temps serait alors constitué par les configurations en constante évolution de toutes les particules élémentaires. Je pense que l'on peut dire que le temps est alors un phénomène émergeant du comportement collectif de particules véritablement élémentaires pour lesquelles le temps n'existe pas . Comment le temps peut-il exister pour une particule vraiment élémentaire s'il reste toujours le même? En d'autres termes, comment peut-il vieillir? Le vieillissement, bon exemple du temps, émerge du comportement collectif des particules élémentaires.

• Comment le temps s'écoule-t-il? Je ne peux pas répondre à cela car le temps ne peut pas s'écouler. C'est, je pense, ce que pensent la plupart des physiciens. Les particules élémentaires en mouvement d'où émerge le temps peuvent évidemment s'écouler. À travers l'espace, avec lequel le temps forme un espace-temps absolu. Subjectivement, on peut percevoir le temps comme "coulant" très lentement (quand on passe un mauvais moment) ou très vite ("le temps passait très vite quand on s'embrassait"), mais c'est une question de mots. Ou regardez la situation où vous rêvez: l'horloge à côté de votre lit indique que cinq minutes se sont écoulées, mais dans votre rêve, il semble que beaucoup plus de temps s'est écoulé. Pour les animaux, la perception du temps peut également être très différente. Mais ceci de côté. La réponse à votre question est donc que le temps ne peut pas s'écouler au sens habituel. Ce qui signifie qu'il n'a pas non plus de direction.

• Pourquoi y a-t-il une flèche du temps? Tout d'abord, permettez-moi de souligner que la flèche du temps n'implique pas que le temps a une direction. La flèche ne pointe pas vers un point dans l'espace. La flèche ne pointe ni du passé vers le futur, car le temps n'a évidemment pas de direction dans le temps. La flèche du temps signifie simplement que le passé est différent du futur, et une flèche est une bonne analogie pour y remédier. La question que vous vous posez est donc: "Pourquoi le passé est-il différent du futur?" Selon la deuxième loi de la thermodynamique, le comportement collectif de toutes les particules de l'Univers est tel que les particules ont tendance à se configurer de plus en plus désordonnées (si la configuration initiale n'est pas dans un état désordonné maximal). Maintenant, par définition, le passé de l'Univers se trouve dans un état plus ordonné que le futur ne se trouve. Vous pouvez vous demander ce qui se passerait si les mouvements de tous les champs de particules étaient inversés (ce qui ne peut être fait que dans l'esprit, mais le regretté Stephen Hawkins a pensé une fois que cela se produirait si l'Univers passait d'une expansion à une contraction, une pensée dont il a par la suite admis heureusement qu'elle était fausse). Quelque chose à quoi penser!

• Si vous souhaitez une réponse courte, alors:
  • Les physiciens désignent principalement un axe de coordonnées lorsqu'ils parlent de temps. Dans la théorie de la relativité, nous mesurons également le temps en mètres!
• Comment le temps s'écoule-t-il?
  • Je dirais plutôt: comment ça se passe. Dans la théorie de la relativité, nous « supposons » que le temps passe avec la vitesse de la lumière. Nous définissons le sens du temps par cette ' définition ':
    • La direction du passage du temps est la même que celle où l ' entropie se développe. Si vous ne savez pas ce qu'est l'entropie, alors en un mot, l'entropie est une mesure de la désorganisation de la matière. Le temps passe donc dans la direction où la désorganisation des particules de notre univers augmente.

C'était une réponse courte et pas extrêmement précise, mais si vous voulez une explication plus approfondie de ces choses, vous pouvez lire beaucoup de livres et regarder beaucoup de vidéos sur youtube sur ce sujet. J'espère que ma réponse a été utile.

J'adopterai un point de vue différent des autres réponses. L'écoulement du temps peut être utilisé en relativité.

Quelques réponses ci-dessus et cette réponse à Est-ce qu'il faut vraiment un temps infini (à l'observateur) pour qu'une personne tombe dans un trou noir? point à temps comme dans le Bloquer l'univers. L'espace-temps est un bloc 4D immuable. Le temps ne passe pas.

Selon cette réponse, Comprendre les phénomènes émergents dans l'univers des blocs. (Question reformulée), pour qu'un flux de temps existe, il faudrait qu'il y ait un paramètre physiquement significatif $ \ lambda $ qui définirait le flux via $ dt / d \ lambda $ sur le bloc 4D. Il n'y a pas de flux. Les gens définissent un paramètre affine comme celui-ci tout le temps en relativité générale, mais il n'a aucune signification physique.

Dans cette optique, je suis quelque chose comme un rouleau de film. Chaque image est moi à un moment particulier. Chaque image existe indépendamment, quelle que soit l'image qui est "maintenant" ou si le film est en cours de lecture ou non. Dans chaque image, je suis dans un état qui ressent l'écoulement du temps et me souvient du passé.

Cependant, comme cette réponse à Comment la position d'une particule peut-elle être aléatoire et incertaine en mécanique quantique si elle est déjà prédéterminée en relativité? le montre clairement, ceci vue ne signifie pas que l'avenir est prédéterminé d'une manière incompatible avec la mécanique quantique. Quelle que soit la nature des fonctions et mesures d'ondes de mécanique quantique, les événements qui en résultent peuvent être disposés dans un bloc d'espace-temps 4D. Le bloc est un moyen pratique de visualiser les événements à des fins de relativité.

De nombreux physiciens adoptent le point de vue selon lequel l'univers de bloc est la façon dont l'univers fonctionne. Mais comme l'a dit John Rennie dans sa réponse, il y a d'autres points de vue selon lesquels il ne s'agit que de sottises mathématiques, et que le temps passe vraiment.

Par exemple, les simulations numériques relativistes générales utilisent souvent le formalisme ADM pour commencer par une condition initiale et calculer les états futurs. L'espace-temps est divisé en feuilles spatiales étiquetées par t. Le tenseur métrique 3D pour chaque feuille est utilisé comme une variable dynamique, avec son moment conjugué. Un hamiltonien peut être dérivé et des équations de mouvement. Les états futurs peuvent être calculés sans les connaître à l'avance.

Tout cela montre que le Block Universe est compatible avec la physique telle que nous la connaissons, malgré sa violation du bon sens. Mais le Block Universe n'est pas nécessaire.

Une partie de la vision de bon sens du temps est qu'il coule. Le présent est tout ce qui existe. L'avenir n'est pas encore arrivé. Le passé est fini et disparu. Je voudrais faire valoir que cela est également compatible avec la relativité. L'écoulement du temps n'est pas requis par la relativité, mais s'il existe, il ne fait aucun mal à la théorie. Pour ce faire, je vais examiner un peu plus en profondeur ce que signifie la simultanéité.

La lumière se déplace à 3 $ \ fois 10 ^ 8 $ m / s. Nous sommes à l'aise avec 3 $ m / s. Nous trouvons la physique relativiste contre-intuitive.

Considérons un monde où le mouvement le plus rapide est 3 $ \ times 10 ^ {- 8} $ m / s. C'est environ 1 m / an, la vitesse d'un glacier. Les physiciens du monde glaciaire se déplacent trop lentement pour voir les effets du mouvement avec lesquels nous sommes à l'aise. Nous pouvons en apprendre davantage sur nos difficultés conceptuelles en regardant ce qu'ils trouvent contre-intuitif dans la physique quotidienne.

Dans la physique classique du monde des glaciers, chaque objet a une propriété intrinsèque fixe appelée position. Chaque observateur s'accorde sur la position d'un objet donné. La position peut être utilisée comme identité de l'objet.

Cependant, des mesures précises ou des mesures sur de longs intervalles de temps montrent que la position change avec le temps. Cela conduit à des concepts contre-intuitifs comme «l'échec de la même place» et la «vitesse».

Ceux-ci peuvent généralement être ignorés. Mais les observateurs voyageant à des vitesses quotidiennes verraient des effets étranges. Les physiciens des glaciers Bob et Alice conviennent tous deux qu'ils ont tous les deux la position $ x_0 $ au moment $ t_0 $ . À $ t_1 $ , Bob dit qu'il a la position $ x_0 $ , comme on pourrait s'y attendre. De même, Alice dit que tout est normal avec elle. Mais Bob dit qu'Alice est à $ x_1 $ .

Cela prête à confusion. Ni Bob ni Alice n'ont changé leur position immuable. Et pourtant, ils sont maintenant à deux positions différentes. Ces positions sont-elles en quelque sorte les mêmes? Est-il en quelque sorte possible d'occuper deux postes en même temps?

Nous avons une confusion similaire sur l'échec de la simultanéité. Nous pensons que le temps est absolu. Un temps $ t_0 $ identifie de manière unique une tranche d'espace-temps. Lorsque $ t_0 $ est maintenant, tous les événements de cette tranche ont leur moment d'existence. L'état de l'univers est spécifié de manière unique par $ t_0 $ . Tous les observateurs sont d'accord sur ce point. L'écoulement du temps est la progression de l'état universel de cause à effet. C'est pourquoi l'écoulement du temps a du sens.

Cependant, les mesures montrent que la vitesse de la lumière est constante. Cela conduit à l'échec de la simultanéité. Les physiciens de tous les jours Robert et Alicia se croisent à une vitesse relativiste. Les deux choisissent des systèmes de coordonnées qui conviennent qu'ils passent à $ (x_0, t_0) $ . Ils regardent l'événement que Robert voit comme $ (x_1, t_0) $ . Robert dit que c'est maintenant son moment d'existence. Alicia dit que le même événement s'est déjà produit ou ne s'est pas encore produit. Cela conduit à la confusion. Un événement se produit à deux moments différents.

L'univers Block est un moyen de contourner cela. Si un événement existe à deux moments différents, il ne doit pas avoir d'existence momentanée. Il doit exister chaque fois qu'il est temps pour qu'il existe dans n'importe quel cadre de référence. Cela préserve la notion que tous les événements dans une tranche d'espace-temps définie par un temps existent à ce moment-là. Cependant, cela détruit la notion de temps qui s'écoule. Une succession d'événements ne naissent pas et disparaissent. L'ensemble du bloc d'événements dans tout l'espace-temps existe de manière statique.

Une autre manière consiste à abandonner l'idée que la simultanéité est absolue. Chaque objet suit une ligne du monde où le temps s'écoule. Chaque événement vécu par un objet prend naissance à son moment et disparaît. Mais il n'y a pas de moyen universel de faire correspondre les temps d'événements séparés. La correspondance dépend autant du mouvement que la correspondance de la position d'événements séparés.

C'est une pierre d'achoppement conceptuelle beaucoup plus difficile pour nous que toute autre chose en relativité restreinte. Nous sommes habitués à ce que Robert voit deux événements comme au même endroit, mais Alicia les voit comme différents à cause de son mouvement. Mais Robert voyant deux événements en même temps et Alicia les voyant comme différents à cause de son mouvement viole notre notion de l'heure. Il est difficile de s'habituer à l'idée que le temps n'est pas ce que nous pensions.

Cela ne change pas ce qu'est la simultanéité en relativité. La simultanéité de deux événements séparés mesurés dans un référentiel inertiel particulier peut être déduite. Robert, assis à $ x_0 $ , peut toujours compter sur son horloge à $ x_0 $ pour être uniforme. Il envoie une impulsion de lumière qui se reflète sur un événement à $ x_1 $ et revient. Il enregistre les heures d'envoi et de retour. La vitesse de la lumière est constante, de sorte que l'impulsion passe la moitié du temps à s'éteindre et la moitié à revenir. La réflexion est donc simultanée à l'événement que Robert a vécu à mi-chemin.

La différence entre les points de vue Block Universe et Flowing Time est purement philosophique.Ils utilisent tous les deux les mêmes diagrammes spatio-temporels, font les mêmes calculs et aboutissent aux mêmes réponses.Un point de vue considère le diagramme espace-temps comme un bloc d'événements statiquement existants.L'autre le considère comme une collection d'histoires vaguement assorties.

Les deux notions de temps sont différentes de la notion de bon sens.Je ne connais aucune expérience qui puisse distinguer ces interprétations du temps.Utilisez celui qui vous rend le plus confortable.

Cependant, il y a une différence.L'univers de bloc n'inclut pas la progression de l'état du début à la fin.Il faut l'ajouter.Il y a une question de savoir comment le motiver et expliquer la direction.Le flux du temps n'explique pas cette progression.C'est juste supposé.

Bien sûr, la réponse de John Rennie est juste, ainsi que la réponse de John Duffield. Les deux réponses sont pour la plupart correctes et techniques. Mais laissez-moi essayer de l'expliquer d'une manière plus simple. Alors, permettez-moi d’essayer d’ajouter quelque chose en l’expliquant de manière très simple et compréhensible et en comparant les deux réponses là où elles sont d’accord et où pas.

1. WQuel est le temps?
   Par John Rennie:

   c'est ce que les physiciens veulent dire, par définition des quatre vecteurs, et que le temps est une coordonnée dans ce système à 4 dimensions que nous appelons l'espace-temps.

   
   Par John Duffield:

   c'est le mouvement des pièces de l'horloge.

   
   Les deux ont raison. Mais les deux essaient de le prendre sous un autre angle. Prenons-les un par un, en essayant de les unifier.

La première réponse dit que l'univers est configuré ainsi et que les quatre vecteurs sont configurés de sorte que le temps en tant que dimension soit juste une autre dimension comme les 3 dimensions spatiales que nous percevons facilement. Maintenant c'est correct et ce n'est que la mesure de l'espace-temps. Il explique que tout mouvement (vitesse) dans les dimensions spatiales est affecté par (et vice versa) le mouvement (vitesse) dans la dimension temporelle. Si quelque chose se déplace à une vitesse $ c $ dans l'espace, il ne doit pas se déplacer dans le temps (sa vitesse dans la dimension temporelle est 0). Si quelque chose se déplace plus lentement que la vitesse $ c $ dans l'espace, il doit commencer à se déplacer dans la dimension temporelle. Ce n’est qu’un fait empirique, et c’est ainsi que l’univers et les quatre vecteurs sont mis en place.

Cela se résume également à l'univers des blocs, où toutes les «tranches de temps» existent déjà, et nous les percevons simplement lorsque nous «nous déplaçons» le long des coordonnées de la dimension temporelle.

À présent, il n’existe pas de théorie acceptée sur ce en quoi tout consiste et sur la façon dont la masse de repos est obtenue, mais une théorie est que les particules sans masse ( gluons) oscillent à la vitesse c dans un certain confinement.

Dans SR, la dilatation du temps est dans un exemple expliquée par une horloge à photons, avec deux miroirs et un photon se déplaçant entre (comme oscillant) les miroirs (un certain confinement). Donc, si nous prenons cela comme une analogie, nous pourrions dire que le temps est le mouvement (dans l'espace) du photon ou le gluon entre les miroirs ou le confinement. Ainsi, tout ce qui existe peut être constitué de petites horloges à gluons.

La première réponse pourrait donc conduire à dire que par le mouvement (oscillation) des gluons des petites horloges et leur vitesse dans l'espace (oscillant à vitesse $ c $ ) affecte leur vitesse dans la dimension temporelle (vitesse 0, temps figé). Ainsi, les quatre vecteurs montreront que ceux-ci ne bougent pas dans le temps.

Mais dès que nous regardons les particules de niveau supérieur qu'elles accumulent, elles, en raison du confinement, gagnent en masse de repos vers les particules de niveau supérieur, et celles-ci (les particules de niveau supérieur) ralentissent dans l'espace. Ils doivent donc commencer à se déplacer dans la dimension temporelle, et c'est ce que leur quatre vecteurs montrera, ils se déplaceront dans la dimension temporelle avec une vitesse> 0.

C'est donc là que la première réponse se connecte à la deuxième réponse, elle dit que le mouvement (vitesse) dans les dimensions spatiales a affecté le mouvement (vitesse) dans la dimension temporelle.

La deuxième réponse dit que le temps n'est que le mouvement des pièces d'une horloge. Donc, fondamentalement, il accepte la première réponse en disant que tout est comme une horloge à photons et que le mouvement dans l'espace affecte le mouvement dans le temps.

2. DLe temps s'écoule-t-il? Non, les deux réponses disent non, car ce n'est pas le temps qui passe, c'est nous qui bougeons le long des coordonnées de la dimension temporelle.

La première réponse dit explicitement que nous évoluons dans la dimension temporelle et que cela ressemble plus à un univers bloc, où tout existe déjà.

La deuxième réponse dit que le temps n'est que des particules en mouvement, donc le temps lui-même ne s'écoule pas mais les particules bougent et c'est ce que nous percevons comme l'écoulement du temps.

La première réponse est juste.c'est ainsi que se mettent en place l'univers et les quatre vecteurs.Permettez-moi de vous montrer pourquoi la deuxième réponse est fausse, et pour ce faire, je dois expliquer quelque chose que aucune de ces réponses ne mentionne.

3. Le cas où aucune de ces réponses n'explique est: si tout dans l'univers (toutes les particules, l'énergie) ne se déplaçait pas dans l'espace (elles seraient stationnaires dans les dimensions de l'espace).

Dans ce cas, la première réponse dirait qu'en se basant sur les quatre vecteurs, nous verrions toujours que tout se déplace dans la dimension temporelle à une vitesse $ c $ .C'est exactement ce que disent les quatre vecteurs, et c'est empiriquement vrai.

La deuxième réponse impliquerait que dans ce cas, puisque rien ne bouge dans l'espace, nous ne percevons pas le temps, et il n'y a pas de temps, il n'existe pas. Mais ce n'est pas vrai. La deuxième réponse est basée sur une idée fausse. Cela implique que les particules se déplacent dans l'espace et que notre vitesse (qui a une masse au repos) est normale, et que nous aurions besoin d'accélérer (dans les dimensions de l'espace) à la vitesse de la lumière. Ce n'est pas vrai. Tout ce qui est sans masse dans l'univers se déplace à une vitesse $ c $ dans l'espace (et se déplace à la vitesse 0 dans la dimension temporelle) dès sa création. Puisque nous pourrions utiliser l'analogie et dire que tout est constitué de petites horloges à photons (gluons), celles-ci se déplacent toutes dans l'espace à une vitesse $ c $ à mesure qu'elles sont créées. S'ils gagnent en quelque sorte de la vitesse pour les particules de niveau supérieur qu'ils accumulent (en oscillant dans un certain confinement), ils ralentissent ces particules de niveau supérieur dans l'espace. C'est la seule façon de se déplacer plus lentement que la vitesse $ c $ dans l'espace, pour ralentir. Au fur et à mesure qu'elles ralentissent, en gagnant de la masse, elles (les particules de niveau supérieur) commencent à percevoir le temps comme nous (qui ont une masse au repos), et commencent également à se déplacer dans la dimension temporelle.

Maintenant, si nous ralentissons tellement que nous devenons stationnaires dans l'espace, ce n'est tout simplement pas spécial. Nous progressons alors toujours à la vitesse $ c $ dans la dimension temporelle. L'idée fausse que vous voyez est que vous pouvez penser que la vitesse 0 dans l'espace est spéciale (pour considérer son effet sur la vitesse dans la dimension temporelle). Ce n'est pas. La vitesse 0 dans l'espace est exactement la même (son effet sur la vitesse dans la dimension temporelle) que n'importe quel autre speed< $ c $ dans l'espace. La seule vitesse dans l'espace qui a un effet spécial (sur la vitesse dans la dimension temporelle) est la vitesse $ c $ . Mais c'est la seule vitesse que les particules sans masse peuvent avoir et si quelque chose veut se déplacer plus lentement, il doit ralentir en gagnant de la masse.

La deuxième réponse est donc fausse, quand elle dit que les particules se déplacent dans l'espace et que c'est ce que nous percevons comme l'écoulement du temps. Parce que, même si rien ne bougerait dans l'espace, nous nous déplacerions toujours dans la dimension temporelle à la vitesse $ c $ .

Comment est-ce possible? La seule solution est vraiment l'univers en blocs, où les versions de notre univers existent toutes dans la dimension temporelle, et nous nous déplaçons simplement le long de la dimension temporelle et réalisons la version réelle de notre monde.

Mais qu'est-ce qui nous fait tous percevoir le même univers en même temps? Comment évoluons-nous tous ensemble dans la dimension temporelle? La réponse est: parce que nous nous déplaçons tous à la même vitesse (approximativement, en volant avec la Terre lorsqu'elle se déplace dans l'espace) dans le même champ gravitationnel. Dès que nous sortons du champ gravitationnel de la Terre, nous percevons le temps à une vitesse différente (puis celles laissées sur Terre), car nous nous déplacerons dans la dimension temporelle à une vitesse différente à cause de GR. Et dès que nous volons à une vitesse différente dans l'espace, (dans un vaisseau spatial rapide) nous percevons le temps différemment (puis ceux qui restent sur Terre) à cause de la SR.

OK, mais comment pouvons-nous nous déplacer dans la dimension temporelle à des vitesses différentes en premier lieu? Comment alors quelqu'un peut-il s'éloigner de la Terre et revenir au même point dans la dimension temporelle que ceux qui sont restés sur Terre? La réponse est que si quelqu'un s'éloigne de la Terre, sort du champ gravitationnel et se déplace à une vitesse différente de celle de la Terre, alors cette personne s'éloigne dans les quatre dimensions. Pour revenir au même point dans les quatre dimensions et rencontrer celles laissées sur Terre au même point dans la dimension temporelle également, il doit utiliser une énergie supplémentaire pour compenser la différence. Sinon, cette personne ne reviendrait sur Terre qu'au même emplacement spatial mais jamais au même point dans la dimension temporelle que celles laissées sur Terre (puisque sa vitesse dans la dimension temporelle est différente). On verrait cela comme s'il aurait vieilli moins (ou plus).

La première réponse est donc juste parce que même si quelque chose est stationnaire dans l'espace, il peut toujours être dans un champ gravitationnel, et cela change sa vitesse dans la dimension temporelle (par rapport à celles en dehors du champ gravitationnel).

Ce n'est pas mon sujet, et je ne suis pas du tout un expert ici, mais je crois que dans des circonstances supplémentaires dans un trou noir, le temps pourrait même s'arrêter (leur vitesse dans la dimension temporelle est de 0 ) pour ceux à l'intérieur du trou noir (du point de vue d'un observateur lointain), et ils peuvent sembler coincés à un certain point dans la dimension temporelle. Il peut donc y avoir un cas particulier où la vitesse dans la dimension spatiale est 0 et dans la dimension temps aussi (pour un trou noir non rotatif à la singularité). Pour recommencer à bouger dans la dimension temporelle, ils devraient utiliser une énergie supplémentaire pour sortir de l'effet gravitationnel du trou noir et commencer à se déplacer dans les dimensions spatiales et temporelles.

J'ai été écarté de ma question (elle est perçue comme un double de celle-ci), je vais donc laisser une réponse ici en guise de photo de départ. John Rennie mentionne que le temps s'écoule dans une direction au rythme d'une seconde par seconde. C'est bien à dire, mais il existe un nombre infini de variations de ce taux dans notre seul univers.

Même pour nous-mêmes en tant qu'individus, le taux semble changer en fonction du fonctionnement de notre cerveau. Nos cerveaux ont différents engrenages (types d'ondes alpha, bêta, gamma, delta [et peut-être plus]) et selon la combinaison d'entre eux en cours, le temps peut sembler se déplacer plus lentement ou plus rapidement. Lorsque nous sommes multi-tâches, nous voulons qu'il ralentisse et lorsque nous nous ennuyons, il semble glisser.

Mais assez de philosophie déjà - nous parlons ici de physique du temps qui est fondamentalement la physique de quelque chose qui n'existe pas. Je ne me souviens plus de qui il s'agit, d'une célébrité en fait mais la personne subit une petite anomalie, une condition "médicale" et elle n'a pas une perception du temps comme le reste d'entre nous (quel que soit le% de la race humaine).

Tout comme certaines personnes n'ont pas de réflecteurs d'appétit qui leur disent quand ils ont suffisamment mangé (des gens en sont morts) la personne que j'oublie qui ne peut pas juger du temps. Alors, sont-ils dysfonctionnels ou plus en phase avec la nature que certains?

Je ne pense pas que les animaux aient une perception du temps. Je pense qu'ils perçoivent les événements et peuvent s'en souvenir (en fait et étrangement, des expériences ont prouvé que les oiseaux peuvent transmettre des «souvenirs» de personnes menaçantes spécifiques à leur progéniture et que les enfants réagissent en conséquence aux personnes sans les rencontrer auparavant) - cependant seuls les humains ont un résumé conception du temps comme "chose".

En fait, dans Henri IV de Shakespeare, le protagoniste se moque d'un imbécile parce qu'il se réfère abstraitement au temps. Le genre de morale est que les gens qui ont le temps de s'interroger sur le temps ne réussissent pas vraiment beaucoup. Cela a été écrit il y a 400 ans et maintenant (riant de moi-même) je fais la même chose. Donc je suppose que je ne le ferai pas après cette petite réponse.

Récemment, en écoutant Julian Barbour (qui a donné une solution au problème des trois corps), il dit en quelque sorte la même chose. Il nous dit que le temps tel que nous le voyons est une sorte de restes d'événements qui ne correspondent pas parfaitement. Comme si vous êtes censé rencontrer un ami et qu'il arrive au lieu de rendez-vous après que vous puissiez commencer à remarquer le passage du temps. Si vous vous étiez rencontrés simultanément, votre esprit aurait pu rester pleinement engagé dans la vie et le temps n'aurait pas été important.

Pour donner un exemple similaire, un mec a dit qu'il avait rencontré une fois Bruce Lee (l'artiste martial) dans un ascenseur et qu'ils avaient commencé à discuter de Kung Fu. Ils sont arrivés au même étage alors ils ont essayé quelques mouvements. La prochaine fois que le mec regarda sa montre, il était 7 heures du matin. Il est monté dans l'ascenseur à 22 h 35, donc le temps disparaît lorsque nous ne le regardons pas.

Semblable à la mécanique quantique, si nous nous endormons, nous pouvons compter que notre réveil fiable fonctionnera (comme le dit John Rennie) une seconde par seconde toute la nuit jusqu'à ce qu'il nous réveille de l'inconscience. MAIS nous n'avons aucun moyen de prouver que c'est ce qui se passe réellement. Tout comme une fonction d'onde non réduite, que fait le temps lorsque nous ne regardons pas?

Comment prouver que nous sommes la même personne qui s'est réveillée et qui s'est endormie? Les bouddhistes disent que l'ego est une fonction. C'est temporaire et parfois il y en a, parfois non. C'est la signification réelle du "si un arbre tombe dans la forêt et qu'il n'y a personne dans les parages, est-ce que quelqu'un l'entend?" koan. Cela se traduit par "si l'ego n'est pas là pour regarder, y a-t-il un ego?" - enfin, évidemment pas s'il n'est pas là pour un instant. Cela pourrait cependant revenir si la réponse Physics Stack Exchange sur laquelle vous avez travaillé dur reçoit beaucoup de votes négatifs ha ha ha.

Donc, sur terre, la mesure précise du temps la plus proche est celle des jours. Tout le reste est difficile à atteindre par les humains parce qu'ils veulent beaucoup de choses, alors ils commencent à calculer comment les obtenir et cela signifie que nous divisons les événements en parties que nous appelons le temps.

C'est aussi le point de vue de Barbour. Nous avons besoin de percevoir la division pour fonctionner et nous possédons un outil inné de division du temps tout comme nous possédons un outil de division d'identité (l'ego) mais comme on le voit chez les personnes qui ont des anomalies, ce can est absent.

Même une émotion comme la tristesse n'est jamais la même deux fois et comme l'a dit un philosophe célèbre: "On ne saute jamais deux fois dans la même rivière". Je ne sais pas comment mettre fin définitivement à cette randonnée. Je dirai peut-être simplement que nous sommes d'accord pour croire que nous savons tous à peu près ce qu'est une heure et qu'une seconde est une mesure très pratique.

Non, attendez. Je terminerai la réponse par une question. Combien d'entre vous, malgré tous vos efforts, sont arrivés en retard pour un événement, une réunion ou n'ont pas fait quelque chose que vous deviez faire dans un laps de temps précis? Le temps était précisément fixé dans votre cerveau, mais la vie était juste plus grande et plus impersonnelle et hors de votre contrôle à tel point que le concept de temps ne fonctionnait pas.

Mais que sais-je? Je ne suis qu'une horloge. Parfois je coche, parfois je coche.

Les physiciens traitent le temps comme une coordonnée qui peut être attribuée à un événement avec les trois coordonnées spatiales, et utilisent le terme espace-temps pour faire référence à la représentation mathématique en 4 dimensions résultante.

La physique définit effectivement le temps comme un décompte des changements.Plus précisément, une seconde correspond à 9 192 631 770 transitions hyperfines successives d'un atome de césium 133.

Si vous pensez au temps, par conséquent, comme un décompte du changement, vous verrez qu'il ne s'écoule pas, c'est simplement un total cumulé du compteur.Il s'ensuit que le temps augmentera toujours, car un nombre d'instances successives entraîne toujours un nombre croissant.

Qu'est-ce que le temps? Demandez à dix personnes différentes et vous obtiendrez dix réponses différentes. Voilà comment je le comprends. Le mot temps est un terme décrivant le mouvement temporel. Le temps est ce que nous faisons. Le temps ne s'écoule pas, nous chronométrons. Nous ne nous déplaçons pas dans la dimension temporelle, nous chronométrons dans la dimension temporelle. Le temps est un verbe.

C'est notre mouvement d'un moment à l'autre. Les horloges mesurent notre progression. Les horloges mesurent à quelle distance nous chronométrons. Les distances temporelles sont mesurées en secondes, minutes, heures, jours, années, etc. Nous nous déplaçons donc dans la dimension spatiale et nous chronométrons dans la dimension temporelle.

La vitesse à laquelle nous chronométrons est connue sous le nom de vitesse temporelle. Traverser la dimension temporelle n'est pas quelque chose que seuls les humains font. Tout sauf les particules sans masse, les temps.

Maintenant, parce que la dimension spatiale et la dimension temporelle sont liées, plus nous nous déplaçons vite, plus nous chronométrons lentement, mais du fait que nos perceptions sont déterminées par notre vitesse temporelle, nous ne percevons jamais de dilatation du temps localement.

Maintenant, je me trompe peut-être, mais il n'y a aucune preuve scientifique qui suggère que ma théorie est invraisemblable. Corrigez-moi si je me trompe, mais si vous n'êtes pas d'accord, juste parce que cela ne correspond pas à vos opinions actuelles, ne commentez pas.