Le plus simple, dites-vous? Il y en a deux qui me semblent simples à démontrer. Heureusement, quelqu'un sur Internet a déjà passé un certain temps pour nous aider ici à rendre ces choses faciles à illustrer:

1. Les ombres diffèrent d'un endroit à l'autre

Eratosthenes a effectué cette expérience pour déterminer la circonférence de la Terre, en supposant déjà sa sphère forme; accessoirement, la preuve que cela est consécutif à la procédure.

Cependant, une démonstration peut être réalisée par une simple expérience locale (au lieu d'avoir une partie s'aventurer à un point assez éloigné):

Prenez un morceau de carte (A3, ou plus), attachez deux obélisques à la carte par leurs bases et, avec une source de lumière, produisez des ombres - maintenant, pliez lentement la carte pour qu'elle devienne convexe (c'est-à-dire, le côté avec des obélisques attachés bombés) et observez l'effet.

2. Vous pouvez voir plus loin de plus haut

Il existe de nombreuses autres façons de démontrer que la Terre est ronde, ou courbée, au moins, en analysant le centre de la gravité à la simple observation des autres objets ronds visibles dans l'espace; mais je pense que ces illustrations sont les plus simples à comprendre.

_{Images provenant de SmarterThanThat}

L'ombre de la Terre sur la Lune lors d'une éclipse et la façon dont les mâts des navires sont encore visibles lorsque les coques sont hors de vue sont les raisons classiques.

Un autre moyen est le triangle rectangle triple :

1. Vous vous déplacez en ligne droite sur une distance suffisamment longue
2. Tournez à droite 90 ° degrés, marchez dans la même direction sur la même distance
3. Tournez à nouveau à droite de 90 ° degrés et marchez à nouveau sur la même distance

Après cela, vous terminerez au point de départ. Ce n'est pas possible sur une surface plane car vous ne feriez que «dessiner» un carré incomplet.

Source: http: //www.math .cornell.edu (ajoutez /~mec/tripleright.jpg pour trouver l'image)

Si la personne en question vient d'une latitude tempérée, emmenez-la sous les tropiques pour ressentir la chaleur du soleil de midi, de préférence piégée sur un voilier sans eau. Montrez le soleil très haut et faites valoir votre point de vue quand ils sont les plus misérables. Ensuite, amenez-les à une latitude très élevée. Alors qu'ils gèlent et s'épuisent à 3 h du matin en marchant dans la toundra, montrez-leur le soleil bas, non couché (ou non levant), et réitérez votre point de vue dans leur état de misère accru. A travers la souffrance et un sentiment de fierté, l'objet de votre démonstration aura probablement maintenant le sentiment d'avoir "été là" et de "l'avoir vu" de "ses propres yeux". Si elle est convaincue, cette personne fera volontiers du prosélytisme sur la "vérité" de la rondeur susmentionnée de ladite planète, et affrontera les hérétiques qui ne croient pas.

Je pense qu'il n'y a pas de réponses simples pour fournir une "preuve" de quoi que ce soit. La «preuve» est relative, tout comme la «vérité» est relative. Si simple signifie "sans utiliser la science ou la technologie", alors vous êtes sans espoir, car le destinataire de la "preuve" doit accepter la vérité de la méthodologie.

Les photos de l'espace sont retouchées.

Les navires en mer regardent sous l'horizon car Osirus / Neptune / Odin / Jesus / Bhaal ne souhaite pas que l'homme voit à l'infini (ce qui prouve aussi que les corps célestes ne sont pas très loin).

Bâtons dans la terre et les ombres ne prouvent rien à moins que vous n'acceptiez que les autres corps soient permanents, en mouvement orbital et éloignés (à quel point la personne croira déjà que la planète est ronde).

N'essayez pas de prouver quoi que ce soit. Vous ne pouvez pas. Au lieu de cela, "Démontrez et éduquez", car tout ce que vous pouvez faire est de convaincre, pas de prouver.

Le fait de rester assis pendant un moment au bord de la mer devrait indiquer clairement que la Terre n'est pas plate, même si vous ne voyez pas de navire passer à l'horizon. Le bord du monde-disque de la Terre devrait être à seulement quelques kilomètres de là, et il est impossible que le monde circulaire tout entier s'intègre dans le cercle que l'horizon océanique semble former.

Les humains n'ont pas seulement connu que la Terre était sphérique, mais en fait mesurait son rayon depuis des milliers d'années. http://en.m.wikipedia.org/wiki/History_of_geodesy

En plus de l'option de remonter dans le temps, vous pouvez simplement montrer à votre "cousin numbskull" une photo de la Terre prise depuis la lune comme celle ci-dessous.

Vous pouvez construire un pendule simple et observer comment il tourne au fil de la journée. Vous pouvez ensuite mettre un pendule sur un bâton ou quelque chose que vous pouvez faire tourner vous-même afin de démontrer que lorsque vous faites pivoter le bâton, le pendule continuera à osciller dans la même direction. Cela montre que la direction du mouvement du pendule ne changera par rapport à sa base que si sa base est tournée.

Les pendules peuvent également être utilisés pour mesurer votre latitude (sa direction changera à des taux différents pour différentes latitudes), et pour mesurer la valeur locale de g (la durée pendant laquelle il prend pour passer par un cycle, ou sa période d'oscillation variera avec la gravité).

L'occurrence de midi (c'est-à-dire le passage méridien du vrai Soleil) n'est pas simultanée pour deux observateurs situés le long d'une ligne est-ouest. Hmmm ... d'accord peut-être encore plus simple. Le lever et le coucher du soleil ne sont pas simultanés pour ces deux observateurs.

I think the simplest way is to have two sticks of same size put both of them perpendicular to the surface of the earth in the mid day sunshine and the gape between them is to be few miles and exact time mesure the angle of elevation or mesure the size of the shadow so both will be differ!By several exams in a sysmetic order we can find that the earth is round.

Il y a une vidéo sur youtube d'une île à quelques kilomètres de là, de sorte que lorsque vous voyez l'île depuis une élévation, vous pouvez voir plus loin à sa base que lorsque vous voyez l'île depuis le rivage (une démonstration de la réponse 1 au dessus). Je pense que c'est le moyen le plus simple étant donné que maintenant nous avons la capacité de zoom, n'importe qui peut faire ce genre d'expérience par temps clair depuis n'importe quel rivage en regardant quelque chose à quelques kilomètres de là.

http: // www.youtube.com/watch?v=bco_p4V7-QU&feature=related

Classiquement, la force gravitationnelle subie par une masse $ m $ au-dessus de la Terre est donnée par le familier,

$$ F = G \ frac {Mm} {r ^ 2} $$

où $ M $ est la masse de la Terre. En d'autres termes, une masse subira une force qui diminue continuellement à mesure qu'elle s'éloigne de la Terre. Supposons maintenant que la Terre soit un grand plan infiniment plat $ ^ {\ dagger} $ dans $ \ mathbb R ^ 3 $ qui est infinitésimal, avec une densité de masse $ \ sigma $ (par unité de surface, pas par volume). Le potentiel gravitationnel $ \ Phi $ satisfait l'équation de Poisson $ \ nabla ^ 2 \ Phi = 2 \ pi G \ sigma \ delta (z) $, en supposant que le plan est à $ z = 0 $.

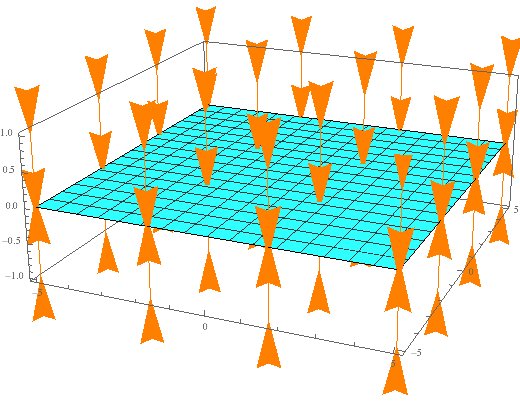
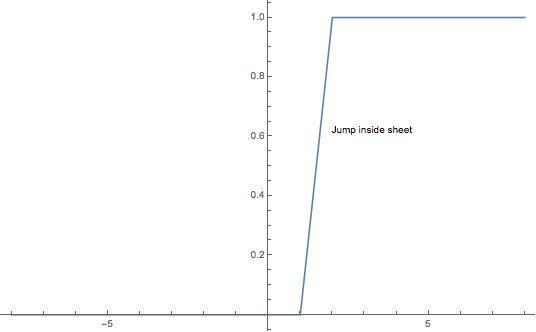
La solution est donnée par $ \ Phi (z) = 2 \ pi G \ sigma | z | $. La force gravitationnelle est $ - \ partial_z \ Phi $, qui pointe toujours vers le plan. Une autre caractéristique est que la force gravitationnelle est constante avec une magnitude $ 2 \ pi G \ sigma $. En d'autres termes, quelle que soit sa hauteur au-dessus du plan, la même force est ressentie. Pour être plus réaliste, si l'avion avait une épaisseur non nulle, la force serait toujours constante, mais à l'intérieur, il y aurait un 'saut' comme illustré:

Par conséquent, pour déterminer si la Terre est plate, il faudrait simplement mener une expérience pour voir comment la force gravitationnelle évolue à mesure que l'on augmente l'altitude. On trouvera $ F \ sim r ^ {- 2} $ approximativement, comme prévu, confirmant que la Terre est ronde. Bien sûr, pour des variations suffisamment petites de $ r $, on peut se tromper en pensant que $ F $ est constant puisque le changement est infime, mais il est mesurable.

$ \ dagger $ Par commodité , il est considéré comme infiniment grand; les conclusions restent les mêmes, mais la force sera bien sûr différente, car elle dépendra également de $ x $ et de $ y $.

dessine un triangle. Sur une surface courbe, la somme des angles d'un triangle n'est jamais égale à 180. Si tel est le cas sur Terre, elle est sphérique.

Si vous êtes dans l'hémisphère nord, marchez vers le sud et remarquez comment le Polaris descend de plus en plus bas chaque nuit jusqu'à ce qu'il disparaisse sous l'horizon.S'il peut gérer plus d'informations, montrez-lui comment les étoiles avant de monter et les étoiles derrière vous diminuent.Bien sûr, vous devrez également expliquer leurs mouvements d'est en ouest.

Voici une autre méthode, qui ne fonctionne que dans l'hémisphère sud - du moins c'est le cas si vous utilisez la carte du monde de la Flat Earth Society, où l'Antarctique est un anneau de glace autour des œuvres, et le pôle Nord est au centre.

Lorsque vous voyagez de Sydney à Santiago ou à Pretoria, vous vous approchez régulièrement suffisamment de l'Antarctique pour le voir.Si la terre était plate, cela signifierait un énorme gaspillage de carburant.Ce n'est que sur un monde sphérique que ce type de trajectoire a du sens.Sur une terre plate, la distance la plus courte entre Sydney et Santiago passe par le pôle Nord, Sydney à Pretoria vous emmène à travers l'Himalaya.

Bien sûr, cela dépend des compagnies aériennes qui essaient d'économiser du carburant - si toutes sont de mèche avec la NASA et tous les autres conspirateurs qui revendiquent une terre sphérique, alors tous les paris sont ouverts ...