Imaginez qu'une personne préfère mesurer le montant d'argent de son compte bancaire avec la valeur $ V $ . L'équation est $ V = C \ tanh N $ , où $ N $ est le montant réel de l'argent en dollars. Cette personne sera également confuse:

Pourquoi y a-t-il une limite ( $ C $ ) sur le montant d'argent que je peux avoir ? Existe-t-il une loi qui stipule que la valeur de mon argent, $ V $ , ne peut pas être supérieure à $ C $ span >?

La réponse est qu'il utilise simplement une "mauvaise" variable pour mesurer ses actifs. $ V $ n'est pas additif - il s'agit d'une transformation d'une variable additive, $ N $ , qu'il doit utiliser pour que tout ait un sens. Et il n'y a pas de "loi de l'univers" qui limite la valeur de $ V $ - une telle limite est juste le produit de sa propre obstination.

La même chose s'applique à la mesure de la vitesse - c'est la «mauvaise» variable pour décrire la vitesse de mouvement; la vitesse n'est pas additive. La variable "correcte" est appelée " rapidité" - elle est additive et il n'y a pas de limite.

Il y a un merveilleux article dont je me souviens avoir lu et qui n'utilise que l'algèbre de base uniquement pour déterminer la forme la plus générale de la formule pour ajouter des vitesses, basée uniquement sur les principes généraux de symétrie (ce qui fonctionne ici fonctionne aussi là , etc.).

Je ne trouve pas celui-là, mais il est facile de le trouver Rien que de la relativité . Et d'autres qui sont dérivés d'une version initiale de Mermin. ^※

Un autre article avec la même idée (mais différents axiomes spécifiques) est Une autre dérivation de la transformation de Lorentz de Jean-Mark Lévy-Leblond publiée en 1976 (merci bdforbs). ^⁂

Dans le Enfin, il montre que la relativité restreinte familière est la réponse incontournable. Dans l'article, une valeur arbitraire non déterminée $ Z $ en est sortie. Il y a 3 cas: le négatif n'a pas fonctionné (dans l'article dont je me souviens, les maths s'étranglent. Dans l'article lié, ce n'est «pas cohérent», mais Greg Egan a élaboré ce cas en détail). $ 0 $ donne le temps absolu fixe de Galileo, et toute valeur positive donne la relativité restreinte avec une limite de vitesse.

La vitesse est juste . En unités naturelles, il s'agit d'une valeur de $ 1 $ . La raison pour laquelle la vitesse de la lumière (ou de toute chose sans masse) semble être quelque chose de spécifique est sa relation avec d'autres choses. En fin de compte, vous pouvez trouver que la relation appelée constante de structure fine a une valeur particulière.

Votre vraie question est: pourquoi la constante de structure fine est-elle la valeur qu'elle est? La réponse est inconnue. Elle peut être déterminée par un ensemble de règles plus profondes que celles que nous connaissons actuellement, elle peut venir de la physique dont nous n’avons pas conscience, ou elle peut / em> être un pur accident comme le nombre de planètes dans notre système solaire plutôt qu'une loi.

Alors, pourquoi $ Z $ est-il différent de zéro? Eh bien, s'il s'agit d'une valeur aléatoire, elle a une chance extrêmement faible d'être exactement zéro, et la valeur réelle qu'elle a, tant qu'elle n'est pas exactement zéro, définit simplement un facteur de mise à l'échelle et ne signifie vraiment rien.

La richesse de l'Univers tient aux effets émergents des bases: étant donné que le temps est relatif combiné à la mécanique quantique, cela signifie que les antiparticules doivent exister, ainsi que la production de paires et l'annihilation.

Si l'univers n'avait pas de relativité restreinte mais avait un temps absolu fixe, ce serait très différent et nous n'aurions pas le même genre de chose du tout. Tout s'emboîte et, dans l'ensemble, si vous examinez une fonctionnalité profonde, vous trouvez qu'elle est nécessairement basée sur les autres fonctionnalités profondes. C'est tout ou rien: vous ne pouvez pas choisir la vitesse finie de causalité en elle-même, pas plus que vous ne pouvez demander pourquoi un côté d'un triangle a la même longueur.

Notes

※ Le papier lié et d'autres liés (de Mermin?) Utilisez une valeur K d'une manière légèrement différente du Z dans le papier que je ne trouve pas maintenant. Ces méthodes faciles à trouver utilisent également le calcul et les limites, ce qui, à cette fin, n'est pas aussi satisfaisant que d'utiliser l'algèbre seule avec quatre relations supposées dues à la symétrie.

⁂ Le celui dont je me souviens à l'origine utilisé (IIRC)

1. l'espace est le même ici et là
2. si A voit B se déplacer à la vitesse X, B voit A se déplacer à la vitesse X dans le direction opposée. équiv. vers l'espace est le même dans toutes les directions dans un modèle unidimensionnel.
3. les résultats des expériences sont maintenant les mêmes que les résultats des expériences à des moments différents. (identique au # 1 mais pour T plutôt que X)
4. Identique au # 2 mais pour T plutôt que X

Je pense que c'est plus satisfaisant que le Lévy- Article de Leblond, qui prend l'accord universel de causalité comme un axiome.

La meilleure réponse que je puisse trouver est "parce que l'Univers serait fondamentalement imprévisible autrement."

Nous pouvons imaginer l'espace-temps comme une variété à quatre dimensions $ \ mathcal {M} $; les lois de la physique dictent alors comment la matière et l'énergie se comportent sur cette variété. (Pour les besoins de l'argumentation, vous pouvez voir cela comme un vieil espace plat de Minkowski, bien que l'argument se généralise pour inclure également les espaces-temps courbes.) Nous pouvons alors poser la question suivante: "Supposons que je sache comment la matière et l'énergie se comportent dans une partie finie de l'univers à un moment donné $ t = 0 $. Qu'est-ce que cela me dit sur le comportement de la matière et de l'énergie dans l'univers après cette période? "

$ \ hspace {100px} $

S'il y a une limite de vitesse dans l'univers, alors il existe une région de l'espace-temps appelée domaine de dépendance , dans laquelle on peut prédire ce qui se passera après notre moment initial. Il se compose de tous les événements de l'espace-temps dont les cônes de lumière passés ¹ , lorsqu'ils sont remontés à $ t = 0 $, sont entièrement contenus dans la région de l'espace dont nous avions connaissance. Vue en fonction du temps, la région de l'espace située dans le domaine de la dépendance se réduira progressivement à néant, au fur et à mesure que les influences extérieures à notre région initiale (dont nous n'avions aucune connaissance) se propagent vers l'intérieur. Mais si l'univers a une limite de vitesse à tous les points, alors nous avons la garantie qu'il y a un volume fini d'espace-temps dans lequel nous pouvons prédire ce qui va se passer.

S'il y a une vitesse de propagation infinie de l'Univers, alors le domaine de dépendance disparaît. En gros, il n'y a aucun moyen de prédire quoi que ce soit, car les influences causales pourraient se propager de l'extérieur de notre région de données initiales et tout gâcher l'instant après $ t = 0 $. Ainsi, s'il n'y avait pas de limite de vitesse, alors l'Univers serait fondamentalement imprévisible; sans la connaissance de tout qui se passait dans l'Univers à un instant donné, les lois de la physique n'auraient aucun pouvoir prédictif.

J'admettrai librement que ce n'est pas vraiment une réponse à "pourquoi y a-t-il une limite de vitesse?" comme "à quoi ressemblerait l'univers s'il n'y avait pas de limite de vitesse?" Pourtant, un univers sans limite de vitesse est suffisamment étranger et incompréhensible pour me rendre heureux de vivre dans un univers avec un. (Cela a des nuances de l'argument anthropique - peut-être que dans un univers parallèle, une créature incompréhensible fait valoir à quel point ce serait horrible de vivre dans un univers avec une limite de vitesse.)

Enfin, notez que rien dans cet argument ne repose sur la relativité restreinte; tout ce qu'il faut, c'est qu'il y ait une notion de "cône de lumière" en chaque point de l'espace. La limite de vitesse peut varier d'un point à l'autre, ou différer selon la direction, mais tant qu'elle sépare le voisinage de chaque point de l'espace-temps en un passé causal, un avenir causal et des régions causalement non liées (comme avec les cônes de lumière conventionnels en relativité conventionnelle) , alors l'argument suit toujours.

¹ "Light-cône" ici ne signifie pas nécessairement "le chemin de tous les rayons lumineux remontant dans le temps", mais plutôt "les chemins de tous les rayons voyageant à la vitesse limite remontés dans le temps."

La physique est une discipline scientifique où les observations et les mesures sont équipées de modèles mathématiques qui décrivent les données existantes et prédisent avec succès de nouvelles valeurs pour de nouvelles conditions aux limites. Lorsque cela se produit, on dit que le modèle a été validé.

Si de nouvelles expériences et observations falsifient le modèle, il faudra réexaminer les hypothèses et même rechercher un nouveau modèle.

Actuellement, le modèle validé que nous avons pour les particules élémentaires est le modèle standard qui utilise la mécanique quantique relativiste et a été testé d'innombrables fois avec des expériences de laboratoire et d'observation. Ce modèle mathématique, parce qu'il incorpore la relativité restreinte, est d'accord avec l'observation que la vitesse de la lumière est une constante c dans le vide. Certes, la valeur de c est un hasard pour cette discussion. C'est l'existence de la limite qui est remise en question, et la seule réponse possible est: parce que le modèle théorique est en accord avec l'expérience et est très prédictif.

Si de nouvelles données falsifient le modèle standard au point qu'un nouveau modèle théorique soit nécessaire, ce nouveau modèle devra intégrer la structure existante pour les cas où il a été validé, y compris la vitesse limite de la lumière. Le modèle standard deviendrait un cas limite pour la nouvelle théorie, pour les énergies et les conditions aux limites qui ont été validées, de la même manière que la physique newtonienne émerge de la relativité restreinte à la limite des basses énergies.

Maxwell a fait une étude mathématique rigoureuse des propriétés de l'électricité et du magnétisme, et il a prouvé qu'il doit y avoir un phénomène qu'il a appelé ondes électromagnétiques . Selon la théorie de Maxwell, une onde électromagnétique doit se propager à une vitesse constante qu'il a appelée $ c $, et qui pourrait être calculée à partir d'autres constantes physiques connues et mesurables à l'époque.

À cette époque, les scientifiques débattaient activement de la nature de la lumière. Après que Hertz ait démontré l'existence d'ondes électromagnétiques dans une expérience de laboratoire, la théorie de Maxwell est soudainement devenue l'explication la plus appréciée de la lumière.

La chose amusante à propos de la théorie de Maxwell était que la vitesse était relative à celui qui la mesurait. Si vous et moi avons mesuré la vitesse des ondes émanant de la même source, nous devrions tous les deux obtenir le même résultat, quel que soit notre mouvement par rapport à la source ou l'un à l'autre.

Certains physiciens ont trouvé que être troublant, et ils ont essayé différentes façons de le justifier. La grande réussite d'Einstein a été de combiner leurs diverses idées en une seule théorie mathématique cohérente et rigoureuse. L'une des conséquences de sa théorie - prouvée en mathématiques - est que si quelque chose a une vitesse caractéristique qui doit être la même pour chaque observateur, alors personne ne peut jamais observer quoi que ce soit se déplaçant plus vite que cette vitesse.

Ainsi, la limite de vitesse universelle est une conséquence mathématique de certaines constantes physiques mesurables, et pour autant que l'on sache, fondamentales; par exemple, la perméabilité de l'espace libre.

Votre question se résume alors à: "Pourquoi l'univers a-t-il ces propriétés?"

Chaque fois que les physiciens répondent une question «pourquoi», la réponse repose toujours sur des niveaux plus profonds de «pourquoi?»

En physique, vous ne pouvez pas demander / répondre pourquoi sans ambiguïté. Maintenant, nous observons que la vitesse de la lumière est finie et qu'elle semble être la vitesse la plus élevée pour l'énergie.

Des théories efficaces ont été construites autour de cette limitation et elles sont cohérentes puisqu'elles dépendent d'appareils de mesure qui sont basées sur des technologies / sciences qui ont toutes été intégrées. Dans les sciences modernes, on ne se soucie pas de ce qui se passe, mais de ce que mesurent les appareils.

La validation de ces théories permet de dire facilement que il existe une vitesse maximale universelle. En fait, il existe une vitesse maximale pour un objet fabriqué à énergie en mouvement lorsqu'il est mesuré dans un espace statique. Ce n'est pas exact dans un univers en expansion ou dans d'autres contextes relativistes critiques. Ce n'est pas exact s'il ne s'agit pas d'énergie, c'est-à-dire avec l'influence présumée qui serait échangée par les particules intriquées. Même ainsi, on ne peut pas voyager plus vite que la lumière sauf dans les rêves.

La physique moderne est nouvelle. Il s'étend dans toutes les directions. Il est encore difficile de faire une synthèse de tout ce qui est connu, de ce qui est utile et de ce qui n’est pas cohérent et pertinent. Peut-être que la valeur finie de c (et pas seulement c) viendra de l'analyse des champs quantiques profonds, de la même manière que la relativité a suivi la très riche théorie de Maxwell. Pendant ce temps, la communauté scientifique n'est pas au courant d'une telle nouvelle analyse, même si elle a déjà été publiée dans un dépôt obscur.

Cette question a suscité des réponses intéressantes, et j'aimerais également y apporter une contribution. Il devrait être parfaitement clair que nous vivons dans un monde avec une vitesse supérieure finie, et de nombreuses réponses ont abordé les conséquences et les raisons de cela.

Je voudrais cependant souligner un aspect cela semble avoir été complètement oublié dans les autres réponses. Si la vitesse de la lumière était infinie, nous n’aurions pas de lumière du tout.

Pour voir cela, jetez à nouveau un œil aux équations de Maxwell. Notez que dans eux $ c = \ frac {1} {\ sqrt {\ mu_0 \ epsilon_0}} $, donc si vous définissez $ c \ sur \ infty $ alors soit (ou les deux) de $ \ mu_0 $ et $ \ epsilon_0 $ devrait être égal à zéro. Cela tuera efficacement l'existence de champs magnétiques dynamiques.

Surtout, pour la lumière, cela signifie que $ \ nabla \ times B = \ frac1 {c ^ 2} \ frac {\ partial E} {\ partial t} \ à 0 $, donc les champs magnétiques seraient statiques (et d'intensité nulle, rappelez-vous pas de monopôles magnétiques). Ainsi, la seule chose qui reste de l'électromagnétisme serait simplement l'électrostatique.

Physiquement, cela a aussi du sens, si $ c \ to \ infty $ alors la réponse du champ électrique à tout réarrangement des charges serait instantanée, donc il n'y a pas de place (temps?) pour une réponse de champ magnétique.

Aussi, en pensant aux champs magnétiques (et en particulier la force de Lorentz), il est également logique que les champs magnétiques disparaissent. Si $ c \ to \ infty $ il n'y a pas de contraction de longueur, et donc il n'y aura pas de forces de Lorentz sur aucune particule.

Ainsi, quand nous parlons de signaux se propageant infiniment vite, il est douteux de quels signaux nous faisons référence à.

Pourquoi avons-nous une limite de vitesse universelle? Existe-t-il une loi plus fondamentale qui nous explique pourquoi?

Les lois les plus fondamentales sont la causalité et la localité. La causalité exprime le fait (ou l'hypothèse) que les effets ne peuvent pas précéder les causes, et la localité exprime le fait (ou l'hypothèse) que les relations causales fondamentales sont décrites par des équations différentielles.

Étant donné ces deux principes fondamentaux, la logique des mathématiques dicte que les équations différentielles sont soit paraboliques (comme l'équation de chaleur), soit hyperboliques symétriques (comme l'équation d'onde).

S'ils sont paraboliques, il n'y a pas de limite de vitesse. Par exemple, selon l'équation de la chaleur, la chaleur se propage instantanément à des endroits arbitrairement éloignés, bien que supprimée de façon exponentielle avec la distance.

Si elles sont hyperboliques symétriques, la théorie mathématique implique une vitesse de propagation finie. Par exemple, c'est le cas des équations de Maxwell, qui limitent la vitesse des signaux électromagnétiques à un nombre appelé la vitesse de la lumière.

C'est un fait expérimental que la Nature se comporte selon la deuxième possibilité - même indépendante des considérations de la vitesse de la lumière. Il existe des preuves accablantes que tous les processus fondamentaux de la nature sont du type hyperbolique symétrique. Même chaleur - l'équation de chaleur n'est que l'approximation la plus simple, dans laquelle la limite de vitesse est perdue. Mais des dérivations plus sophistiquées de la mécanique statistique hors équilibre produisent des équations hyperboliques symétriques, qui ne deviennent paraboliques qu'après une plus grande approximation.

Que la vitesse limite soit la vitesse de la lumière est très probable mais pas nécessairement le cas. Il est lié à l'hypothèse que les photons sont sans masse. Si les photons étaient massifs mais que les gravitons sont sans masse, la vitesse de la lumière serait inférieure à la limite théorique des vitesses du signal dans l'univers - qui serait alors la vitesse de la gravité.

Cependant, selon l'examen des particules du groupe de données sur les particules, les limites supérieures de la masse d'un photon sont extrêmement minuscules et les observations sont actuellement en plein accord avec l'hypothèse de photons sans masse.

L'existence de la limite de vitesse est liée à l'existence du temps [UPDATE: time est une mesure qui n'est disponible que lorsque $ c $ est limité. Si vous n'êtes pas d'accord, fournissez un moyen de mesurer le temps où $ c $ est infini avant le vote négatif]. S'il n'y avait pas de limite de vitesse, tout se passerait instantanément. De plus, aucune vague, quelle que soit sa matière, ne serait affectée et se propagerait momentanément. Le temps disparaîtrait (ainsi que la distance et, par conséquent, l'espace, btw).

Donc, c'est la même chose que "pourquoi y a-t-il du temps?". Le transfert d'énergie instantané qui est actuellement limité changerait le monde tel que nous le connaissons et ce ne serait plus ce monde que nous connaissons plus. La physique newtonienne disparaîtrait en tant que concept, puisque la matière elle-même ne fonctionnerait plus ainsi. Ainsi que le concept de forme. Les conséquences se feraient sur tout. Cependant, nous n'observons pas cela, nous observons la limite.

Il y a une séparation inhérente présente dans la matière universelle, qui lui permet d'exister de la façon dont nous la connaissons / la percevons. S'il existe un monde sans limite, nous n'y sommes pas apparus, nous sommes apparus ici.

Pas exactement une réponse, mais il n'y a rien d'autre à dire

MISE À JOUR

En réponse au commentaire de @Davors:

Il est difficile d'imaginer ce qui se passerait exactement car nous ne pouvons pas être sûrs de la structure sous-jacente réelle de la réalité qui compense la vitesse de la lumière et comment est-elle liée au reste des choses. C'est - comment les 3 autres forces formeraient la matière si EM était instantanée. Mais explorons quelques options qui soutiennent la notion:

1. Il y a 4 forces, et si la force EM transfère toute l'énergie instantanément, alors même si les 3 autres forces tiennent toujours, cela invaliderait la plupart des structures plus grandes que les atomes de la matière que nous voyons maintenant. Étant donné qu'au niveau macro, seules la gravité et la ME importent, et que la gravité n'aura pas de grand sens dans ce scénario, alors tous les processus conduits via les forces EM seront instantanés.

2. Aucune structure de macro ne pourrait exister, et avec tous les processus EM allant à l'infini, il n'y aurait aucune possibilité de savoir quoi que ce soit sur les états d'électrons dans les atomes. Ils deviendront infiniment tous les états possibles. Toutes les absorptions et émissions possibles se produiront en même temps. Je ne sais pas même si les atomes tiendraient le coup.

3. Essayez de mettre l'infini au lieu de $ c $ dans toutes les relations et voyez ce qui se passe. De plus, comme toutes les vitesses peuvent effectivement être mesurées comme une fraction de $ c $, alors si $ c = \ infty $, toutes les autres vitesses seront également infinies quel que soit le coefficient de fraction.

4. Voir la réponse de @Nikos M.

$ \ hspace {50px} $
L'image ci-dessus, j'ai dessiné pour développer la merveilleuse réponse de Kostya.

En gros, imaginez des gens qui mesurent la taille des bâtiments en degrés d'angle de visibilité des bâtiments à partir d'une certaine distance fixe. Ce n'est pas du tout déraisonnable si vous fixez la distance C suffisamment grande par rapport aux hauteurs du bâtiment ». Cependant, pour les bâtiments plus hauts, vous remarquerez que leur hauteur angulaire n'est pas additive. La hauteur angulaire maximale possible est également fixée à une valeur absolue de 90 degrés.

Ceci est très similaire à la façon dont les humains mesurent la vitesse: nous avons choisi une certaine mesure "distance / temps" qui a du sens pour des vitesses plus petites, mais pour des vitesses plus élevées, ce n'est pas additif. Il y a aussi la vitesse "maximale" inaccessible, la vitesse de la lumière.

Cependant, le problème ci-dessus est uniquement dû au mauvais choix de la vitesse de mesure. Le "bon" choix de vitesse de mesure est la "rapidité", comme l'explique Kostya. Et la rapidité est à la fois additive et illimitée.

Savons-nous POURQUOI il y a une limite de vitesse dans notre univers?

Votre question est similaire à:

"Savons-nous POURQUOI il y a une limite de longueur? "

De la même manière que nous avons besoin de longueurs finies pour mesurer la taille ou l'intervalle entre deux points en 3D - Espace euclidien , nous avons besoin d'un vitesse finie de la lumière pour mesurer l'intervalle entre les événements dans 4D - espace Minkowski . Minkowski a développé sa théorie pour élargir l'équation de Maxwell en quatre dimensions. Pour que $ s ^ 2 $ dans l'espace de Minkowski, (2), conserve son invariance, en tant qu'extension du théorème de Pythagore, (1), qui dans trois dimensions est: $$ s ^ 2 = x ^ 2 + y ^ 2 + z ^ 2 \ tag {1} \ ,, $$

et en quatre dimensions devient: $$ s ^ 2 = x ^ 2 + y ^ 2 + z ^ 2 - {\ left (ct \ right)} ^ 2 \ tag { 2} \ ,, $$ $ c $ doit être non seulement fini mais identique pour tous les cadres de référence, ce qui est étayé par les preuves observées que la lumière (Ondes EM) la vitesse était indépendante du cadre de référence des observateurs.

La vitesse de la lumière doit avoir une limite, c'est-à-dire être finie pour que la Relativité Spéciale fonctionne:

Si vous revenons aux fameuses expériences de pensée d'A. Einstein, plus précisément celle où il y a deux observateurs, l'un ne bouge pas, $ A $ , debout sur une gare et un autre, $ B $ , se déplaçant debout dans un train, qui passe par la gare.

Maintenant, quand le train passe et $ A $ et $ B $ sont juste en face l'un de l'autre, la foudre des deux côtés de $ A $ , à la même distance . $ A $ les voit simultanément:

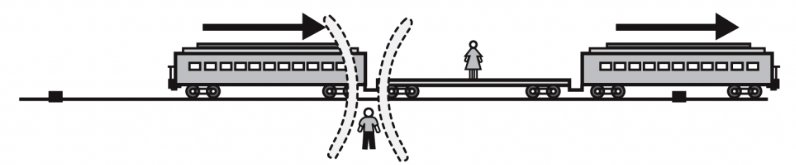
Cependant, parce que $ B $ se déplace par rapport à eux, c'est-à-dire s'éloigne de l'un et vers l'autre il les voit successivement:

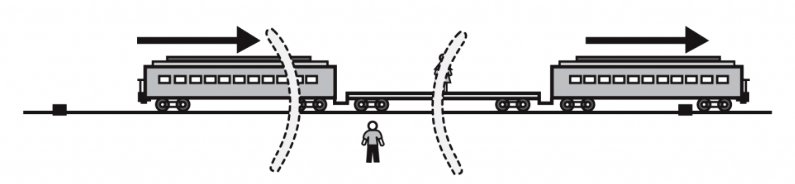
...right?

Eh bien, NON, cela aurait abouti à une mesure différente de la lumière dans différents cadres de référence, ce qui a été réfutée par l ' expérience Michelson – Morley qui utilisait la Terre comme le train :
$ \ hspace {100px} $ ,

et la vitesse de la lumière mesurée dans deux directions perpendiculaires:

en supposant que la lumière se déplaçant dans la direction correspondant à la direction de mouvement de la Terre devrait être plus petite (similaire à la personne, $ B $ , qui était sur le train) que l'autre, hypothèse qui s'est avérée scientifiquement fausse.

Par conséquent, la vitesse de la lumière est constante et quiconque la mesure trouvera la même valeur, quelle que soit sa vitesse ou en d'autres termes vitesse de la lumière est invariant . L'invariance pourrait être comparée à la relativité, par exemple, la relativité du temps, qui était d'ailleurs utilisée pour décrire pourquoi les deux personnes, $ A $ et $ B $ , observez la même vitesse de la lumière, à savoir parce que le temps de la personne en mouvement $ B $ s'écoule plus lentement, en général, plus la vitesse relative entre les deux observateurs est grande, plus la différence de taux de ticking de leurs montres est grande, c'est-à-dire dilatation du temps .

Enfin, la dilatation du temps pourrait être observée en présence d'un objet de masse générant un champ gravitationnel, ou en termes de Relativité Générale dans l'espace-temps étiré, ce qui provoquera le temps de l'observateur situé plus près de l'objet de masse à tic-tac à une vitesse plus lente, c'est-à-dire dilatation du temps et respectivement, l'observateur situé à une plus grande distance observera sa montre tic-tac à une vitesse plus rapide.

Comme vous le voyez, le temps est relatif, l’espace s’étend et la vitesse de la lumière est la constante, avec une valeur finie qui "les maintient ensemble" et "les synchronise" , définir la simultanéité des événements. De plus, avec son aide, nous pouvons définir un intervalle invariant entre deux points dans l'espace-temps, c'est-à-dire entre deux événements . Les intervalles spatio-temporels dépendent des séparations temporelles et spatiales des deux points et peuvent être: de type temps , de type lumière ^{(distance temporelle = distance spatiale )} ou espace-like ^{(distance temporelle < espace distance)} . Grâce à cela, la Relativité Spéciale est une théorie réussie, avec une longue liste de preuves d'expérimentation à l'appui.

Edit:

En réponse au premier commentaire, qui soutient que la dilatation du temps est le résultat de la constance de la vitesse de la lumière, je vais vous présenter un exemple du contraire, c'est-à-dire que la constance de la vitesse de la lumière peut être représentée comme une conséquence directe de la dilatation de la vitesse de la vitesse:

Considérons une horloge hypothétique appelée horloge photon. Dans celui-ci, la lumière est réfléchie dans les deux sens entre ses miroirs et chaque fois que la lumière frappe un miroir donné, l'horloge tourne une fois. Si cette horloge est en mouvement inertiel par rapport à un observateur, alors la dilatation du temps de vitesse la fera, comme tous les autres types d'horloges, tourner plus lentement. Cependant, comme l'horloge est en mouvement, l'impulsion lumineuse tracera un chemin plus long et incliné entre les miroirs. Le résultat net de la dilatation du temps de vitesse et de l'augmentation de la longueur du trajet est que la vitesse de la lumière dans l'horloge à photons en mouvement reste égale à la vitesse de la lumière dans l'horloge à photons de repos. En d'autres termes, la vitesse de la lumière reste constante.

De plus, la transformation de Lorentz (LT), qui a été dérivée par Joseph Larmor [1] en 1897, et Lorentz (1899, 1904) [2], prédisent directement la dilatation du temps. En fait, la dilatation du temps par le facteur de Lorentz a été correctement prédite par Joseph Larmor (1897) [3] bien avant qu'Einstein ne publie son article en 1905.

^{Votre question a tendance à être un peu Philosophique, pour autant que l'on sache, la valeur de $ c $ pourrait être liée à une propriété de l'espace-temps lui-même, déterminée avec les autres Constantes physiques fondamentales pendant le Big Bang, ce qui est difficile à observer et à réaliser, de la même manière que les poissons ne sont pas conscients de toute l'eau qui l'entoure.}

^{[1] Larmor, J. (1897), «Sur une théorie dynamique du milieu électrique et luminifère», Transactions philosophiques de la Royal Society190: 205-300.
[2] Lorentz, Hendrik Antoon (1899), «Théorie simplifiée des phénomènes électriques et optiques dans les systèmes en mouvement », Proc. Acad. Science Amsterdam I: 427-443; et Lorentz, Hendrik Antoon (1904), «Phénomènes électromagnétiques dans un système se déplaçant à une vitesse inférieure à celle de la lumière», Proc. Acad. Science Amsterdam IV: 669-678.
[3] Larmor, J. (1897), «Sur une théorie dynamique du milieu électrique et luminifère, partie 3, relations avec les médias matériels», Phil. Trans.Roy. Soc. 190: 205-300}

Beaucoup de réponses ici se concentrent sur la mauvaise moitié du problème, je pense. Ils vous disent comment nous savons qu'il y a une limite, plutôt que d'expliquer pourquoi il doit en être ainsi.

Pour la plupart, rien n'empêche la création d'un univers avec une vitesse de la lumière infinie qui serait autrement similaire à la nôtre ¹ . Cependant, il y a une propriété importante qu'un tel univers devrait avoir: il doit être fini et / ou non homogène.

Ceci est lié au paradoxe d'Olber. En gros, cela se passe comme suit:

1. La lumière d'une étoile à une distance donnée est inversement proportionnelle au carré de la distance. $ L \ propto {1 \ over D ^ 2} $ .
2. Le nombre d'étoiles à une distance donnée est directement proportionnel au carré de distance. $ N \ propto D ^ 2 $ .
3. La lumière totale des étoiles à une distance donnée est égale à la lumière par étoile multipliée par le nombre de étoiles. $ T \ text {light} $ $ = LN \ text {light} $ $ = L {\ text {light} \ over \ text {star}} N \ text {stars} $ . ("lumière" et "étoile (s)" sont des unités ici.)
4. Par conséquent, la lumière totale d'une distance est la même que la lumière d'une autre distance. $ T \ propto LN $ $ \ propto D ^ 2 {1 \ over D ^ 2} $ $ \ propto 1 $ .
5. Si les étoiles sont réparties de manière homogène dans l'univers et que l'univers est infini, nous pouvons séparer les étoiles en un nombre infini de coquilles, chaque coquille ayant une luminosité finie et constante. La somme de toute cette lumière est infinie. $ \ sum_ {D = 0} ^ {\ infty} T = \ infty $ .

Dans l'univers réel, ce n'est pas un problème à cause de deux effets: premièrement, l'expansion de l'univers signifie que chaque étoile de l'univers s'éloigne de nous (en moyenne), et le taux de récession est directement proportionnel à la distance de l'étoile; et deuxièmement, parce que la vitesse finie de la lumière signifie que la lumière provenant d'étoiles éloignées met plus de temps à nous atteindre qu'elle ne le devrait, en raison de ladite expansion.

Combinée, cela signifie la lumière qui nous atteint par seconde à partir d'une coquille donnée des étoiles descend linéairement avec la distance. $ L \ propto {1 \ over D} $ . En outre, cela signifie qu'il y a une distance finie où tous les objets à cette distance s'éloignent de nous plus rapidement que la vitesse de la lumière, donc nous ne verrons jamais la lumière au-delà de cette distance (rendant effectivement l'univers fini). $ \ sum_ {D = 0} ^ {N, N< \ infty} {T \ over D} < \ infty $ .

Mais si la lumière voyageait à une vitesse infinie, l'expansion n'aiderait pas. Cela signifierait que la luminosité de l'univers diminue lentement (les étoiles sont plus étalées, donc la luminosité par coquille est plus faible), mais une diminution de la luminosité infinie n'aide pas beaucoup. Donc, l'univers devrait être de taille finie et / ou les étoiles devraient être moins denses à mesure que vous vous éloignez du centre.

Alternativement, nous pourrions poser un univers où la lumière s'atténue plus rapidement. $ L \ propto {1 \ over D ^ 3} $ ou quelque chose. Mais cela n'a plus de sens géométrique et nécessite des manipulations supplémentaires pour fonctionner. Peut-être que la lumière est en quelque sorte absorbée par le mécanisme d'expansion, la lumière étant absorbée plus facilement car sa puissance est proche de zéro. L'espace infini signifie que l'absorption lumineuse proportionnellement infinie entraîne un taux d'expansion fini et augmente l'atténuation de la lumière. Mais c'est une sorte de merde d'ondium à la main que j'ai inventée et qui appartient plus à la construction du monde qu'à la physique actuelle.

Même si l'univers était fini, notez que la luminosité de toutes les étoiles de notre propre galaxie surpasserait de loin le soleil. Donc, nous ne pouvons vraiment pas avoir un univers presque identique au nôtre à moins que la lumière n'ait une vitesse finie.

De plus, notez que je ne sais rien de la mécanique quantique ou comment la vitesse de la lumière affecte cette branche de la science . Il est possible que la mécanique quantique actuelle ne puisse exister avec une vitesse de la lumière infinie, ce que vous pourriez déclarer signifie que tout univers avec une vitesse de la lumière infinie est totalement différent du nôtre. ¹ Cependant, je considère que «semblable à notre univers» signifie tout univers avec la physique des particules qui permet la formation de planètes, d'étoiles, de voies neuronales, etc., à un niveau macro qu'un humain typique reconnaîtrait comme similaire. Peu m'importe si "l'or" a plus de protons que "l'hydrogène", etc., beaucoup moins d'effets quantiques.

Je peux sentir à partir de votre question que vous cherchez une explication simple et basique sans jargons. Je vais lui donner une idée honnête et la garder très simple et classique. Je suis un penseur classique, donc je n'ai même pas d'explication plus complexe. J'espère que les utilisateurs plus qualifiés et accrédités ne fronceront pas les sourcils face à la réponse.

Permettez-moi de diviser la question en deux parties -

(1) Pourquoi il y a une certaine vitesse des ondes électromagnétiques (qui se trouve être c)

La vitesse de toute vague est la propriété du milieu à travers lequel elle se déplace. Ainsi, c'est la propriété de l'espace vide que les ondes électromagnétiques se déplacent à une certaine vitesse (ni plus, ni moins). C'est une propriété, pas une limite. Si c'était une limite, alors la lumière (ou EM) pourrait voyager à < c à travers un espace vide. Mais il voyage exactement en c, dans un espace vide. Donc, c'est une propriété.Si vous avez un problème avec cette explication, vous devriez également avoir un problème avec - le son ayant une certaine vitesse dans l'air, et vous devez passer à un niveau plus basique.Si vous acceptez une certaine vitesse du son, je s'attend à ce que vous acceptiez également cette propriété en cas d'ondes EM. La valeur de cette propriété se trouve être c. james large l'a également indiqué, dans sa réponse à votre question du 21 janvier.

(2) Pourquoi un corps matériel ne peut pas se déplacer plus vite que c

Ceci est une conséquence directe de (1) et ainsi, s'avère être une limite. (C'est une limite car les corps peuvent se déplacer à n'importe quelle vitesse tant qu'elle ne dépasse pas c)

Voyons comment augmenter la vitesse d'une masse - nous lui appliquons une force. Par exemple, nous pouvons faire bouger une voiture debout en la poussant avec nos mains. Les électrons dans nos mains et ceux de la voiture (là où nous les touchons) se repoussent et cette force répulsive provoque une augmentation de la vitesse de la voiture. Supposons que vous couriez à votre vitesse maximale et qu'une voiture passe à côté de vous à 300 miles / heure. Pouvez-vous augmenter la vitesse de la voiture en poussant avec vos mains lorsqu'elle passe à côté de vous? La réponse est non (un être humain normal ne peut pas déplacer les mains à plus de 300 miles / h). Pour augmenter la vitesse d'un corps en mouvement, la force doit agir sur lui plus rapidement que la vitesse du corps en mouvement.

Toute force que nous appliquons pour accélérer un corps, la force est finalement exercée sur le corps comme l'une des forces fondamentales. Toutes les forces fondamentales elles-mêmes voyagent en c. À titre d'exemple, la force électromagnétique se propage à la même vitesse que les ondes EM, c'est-à-dire c. Pour simplifier, admettons que toutes les forces fondamentales se propagent en c comme une propriété par (1) Par conséquent, elles ne peuvent pas augmenter la vitesse de tout corps matériel qui se déplace déjà à une vitesse de c à> c.

Remarque que les forces doivent se déplacer plus vite que c dans l'espace pour provoquer une vitesse supérieure à c. Mais nous savons qu'ils se déplacent à c. Ainsi, même les forces fondamentales deviennent inefficaces pour un corps qui se déplace déjà en c.

Les forces deviennent inefficaces dans le sens du mouvement du corps en c. Ils sont toujours efficaces dans d'autres directions et, ainsi le corps peut être ralenti etc.

Par conséquent, la vitesse de propagation des forces fondamentales est une propriété (pas une limite). Cette propriété a la valeur la plus élevée dans l'espace vide qui se trouve être c. Et rien ne peut se propager plus vite que les forces elles-mêmes - qu'est-ce qui en fera quelque chose? La vitesse des forces (une propriété tout comme la vitesse du son) s'avère être une limite de vitesse pour les corps matériels. Ce qui n'est pas du tout un mystère.

Puis-je également commenter que dans les accélérateurs de particules, ils utilisent les champs électriques / magnétiques pour accélérer les particules et ne peuvent évidemment pas les accélérer plus vite que c.

Veuillez LMK si cette explication fonctionne pour vous.

Comme vous l'avez lu dans d'autres réponses, ce n'est pas une chose facile à expliquer. Cela semble tellement contre-intuitif. "Si je veux aller plus vite, pourquoi ne pas simplement accélérer davantage?" ou "Si ma vitesse est très proche de la vitesse de la lumière, alors je tire une balle, ne va-t-elle pas aller plus vite que la lumière? Pourquoi pas?"

Relativité

Commençons par affiner ce que nous entendons par «limitation de vitesse». Disons que vous êtes dans un vaisseau spatial avec une source de carburant infinie et un potentiel d'accélération arbitraire. Vous êtes au repos (amarré à une station spatiale) et vous souhaitez voyager vers un système stellaire à 10 années-lumière. Combien de temps cela vas te prendre? Dans ce vaisseau spatial hypothétique, vous pourriez y arriver en 10 MINUTES, pas en années (en supposant que l'accélération ne brouille pas votre corps humain délicat).

Mais n'est-ce pas une violation de la limite de vitesse cosmique? Nan! Techniquement, vous ne voyagez pas plus vite que la lumière. De votre point de vue, il semble que l'espace s'aplatit et que votre destination se rapproche de vous. Si quelqu'un à la station spatiale vous regardait embarquer, de son point de vue, vous voyageriez très près de la vitesse de la lumière, mais il ne vous verrait arriver à destination que dans moins de 10 ans.

Allons maintenant un peu plus loin et imaginons que vous êtes un faisceau de lumière voyageant dans l'espace. De votre point de vue, combien de temps faut-il avant d'interagir avec quelque chose? Pas de temps du tout. Un faisceau de lumière se téléportera instantanément de la source à une destination sans un passage du temps. Mais bien sûr, les mêmes principes de relativité s'appliquent ici - un observateur extérieur ne connaîtra pas cette téléportation instantanée.

Non-Relativité

Imaginez maintenant un univers alternatif où il n'y a pas de limite de vitesse cosmique. Premièrement, la lumière voyagerait instantanément. Ainsi, lorsque nous regardons le ciel, nous voyons d'autres étoiles et planètes exactement comme elles sont actuellement. Nous pourrions voyager vers et depuis n'importe quel endroit de l'univers dans un laps de temps arbitrairement petit. Cela semble réaliste, n'est-ce pas?

Le problème est ce qui se passe à une plus petite échelle. Imaginez un processus atomique - comme celui de notre Soleil - dans cet univers hypothétique. Le noyau du soleil est d'environ 15 millions de degrés Celsius (rappelez-vous - la température est liée à l'énergie cinétique). Le soleil a un diamètre d'environ 4,6 secondes-lumière.

Une vitesse relativiste de la lumière agit comme un étranglement, empêchant ces réactions atomiques en chaîne de se produire trop rapidement. Cela permet de limiter la chaleur de quelque chose (en augmentant la masse de particules qui se déplacent très vite, pour les empêcher de se déplacer trop rapidement) et la vitesse à laquelle les réactions peuvent se produire (fractions de seconde pour que l'énergie se déplace par rapport à instantané, ce qui est une énorme différence). Cela pourrait signifier que les étoiles explosent trop rapidement pour se former. Cela pourrait aussi signifier que l'énergie qui alimente les réactions s'échappe trop rapidement du soleil et ne lui laisse pas le temps de réagir. Je ne suis pas sûr de ce qui se passerait, mais de toute façon les résultats sont catastrophiques.

Conclusion

La "limite de vitesse cosmique" est un aspect important de notre univers. S'il est concevable de concevoir un univers sans limite de vitesse relative, les résultats ne seraient pas très intéressants. Notre intuition nous dit que cela devrait être possible, mais parfois notre intuition sur des choses que nous ne comprenons pas complètement n'est pas très bonne.

La question "pourquoi y a-t-il une limite de vitesse cosmique?" est aussi fondamental que "pourquoi l'univers contient-il plus de matière que d'antimatière?" ou "pourquoi le magnétisme existe-t-il?". La question doit être reformulée: "Pourquoi vivons-nous dans un univers avec ces caractéristiques?" Ou "Pourrions-nous vivre dans un univers aux caractéristiques différentes?" Parce qu'il est possible que d'autres univers avec des caractéristiques différentes existent, et seule une petite partie d'entre eux peut réellement soutenir la vie. Si la vie humaine existe, elle le fera naturellement dans un univers qui peut la soutenir.

Contrairement aux autres réponses, je vais essayer de donner une réponse simple.

Premièrement, sachez que "Pourquoi" est une mauvaise question pour la science moderne, car la science moderne préfère prédire "quoi" se produira aussi précisément que possible en utilisant des «modèles» de ce qu'ils pensent que la réalité est en train de faire.

La vitesse et le temps sont étroitement liés et sont effectivement sous la même «limite de vitesse». Lorsque vous avancez aussi lentement que possible dans l'espace, vous avancez aussi vite que possible dans le temps et vice-versa.

Notre univers observable semble avoir une limite universelle «d'espace-temps». Cette limite est partie des " constantes fondamentales" interconnectées de notre univers.

Ce qui est intéressant, c'est que si l'une d'elles était modifiée de manière significative, nos modèles actuels prédisent des versions très différentes de la réalité dans laquelle il est très improbable que la vie sensible naisse (veuillez excuser la spéculation sauvage ici) pour pouvoir poser cette question.

C'est ce qu'on appelle le principe anthropique

La réponse à votre question

Savons-nous POURQUOI il y a une limite de vitesse dans notre univers?

est "oui, parce que nous avons la chance de vivre dans un univers ces limites de vitesse apparemment aléatoires ont permis à la vie sensible d'apparaître "

Il peut y avoir beaucoup d'univers de ce type, peut-être avec des constantes fondamentales différentes des nôtres, éventuellement des formes radicalement différentes de vie sensible.

Les vraies questions de PHYSIQUE derrière toute cette philosophie incluent

• "Y a-t-il d'autres univers?"
• "Que peut nous les connaissons? "
• " Quelles sont les distributions de probabilité des constantes fondamentales dans ces univers? "
• etc etc etc

Malheureusement, je ne ne pensez-vous pas que des expériences scientifiques pratiques ont encore été proposées pour tester ces modèles?

Ainsi, ce sujet est plus de la philosophie plutôt que de la physique , donc votre question devrait probablement être fermée comme désactivée -topic?

Le libellé a été mis à jour en réponse au commentaire.

Cette question a une réponse très courte mais utilise l'hypothèse que toute relativité utilise. c'est-à-dire que la vitesse de la lumière est constante pour tous les observateurs.

Sur la base de cette hypothèse, il est trivial de montrer qu'un événement horrison est observé à une vitesse de c en essayant d'accélérer à l'infini.

Pour expliquer pourquoi cette hypothèse est valide, vous devez regarder la dérivation des équations de Maxwell qui montrent que la vitesse de propagation des ondes électromagnétiques est indépendante du cadre de référence. La dérivation de ces équations est fondée sur des concepts tels que la "conservation de la charge" et la loi de Faraday. Je ne crois pas que la question puisse trouver une réponse plus profonde que cela.

tldr: Grâce à la conservation de l'énergie => charge et aux observations emperiques des interactions électromagnétiques, on peut montrer que la vitesse de la lumière est indépendante du cadre inertiel . Cela peut être utilisé pour prouver qu'il existe une limite de vitesse universelle de c.

On peut dire qu'il ne s'agit que d'un résultat expérimental. Cette lumière (et les autres signaux / interactions) ne voyagent pas avec une vitesse / vitesse infinie.

On peut la laisser là et dire que c'est comme ça.

On peut aussi dire, regardez si vous prenez cette variable et effectuez cette transformation (par exemple rapidité ), elle peut être ajoutée à l'infini, donc la question porte sur la variable correcte à utiliser. Bien que cela contourne simplement la question réelle au lieu de l'aborder.

Je vais adopter une autre approche et poser la question directement au cœur.

La vitesse finie de transmission du signal (ou d'interaction) est une exigence de base pour que la causalité soit maintenue .

Sinon, si la transmission du signal peut être infinie, un effet peut dépasser sa propre cause et les boucles causales qui en résultent font la causalité cesse d'être comme causalité. Quelque chose qui est aussi un fait expérimental mais d'un niveau encore plus basique. En ce sens, c'est la réponse à la question.

On peut aller encore plus loin et dériver une transmission de vitesse finie (limite supérieure) directement à partir de considérations thermodynamiques qc qui est en dehors de la portée de cette question, mais le mentionner pour étude ultérieure.

Cependant, la vitesse finie de transmission du signal n'est pas nécessairement équivalente au postulat de relativité spéciale selon lequel la vitesse de la lumière est ce maximum (et constant ) vitesse disponible.

On peut avoir de nombreuses vitesses de transmission finies différentes inférieures à ou même supérieures à la vitesse de la lumière selon le processus à l'étude.

En fait, il existe des recherches sur la transmission de signal plus rapide que la lumière par intrication quantique. Mais je vais juste laisser ça à ce stade

Eh bien, il est possible de prouver (théoriquement, et je vous conseille pour Feigenbaum, 2008) que l'homogénéité et l'isotropie de l'espace et l'homogénéité du temps conduisent nécessairement à l'existence d'une limite de vitesse .

Faisons cela: imaginez prendre l'Univers et supprimez (supprimez) tous les types d'objets. Vous ne restez qu'avec l'espace-temps lui-même. Dans cet espace-temps il n'y a rien, peu importe pas d'énergie.

Maintenant: est-il raisonnable de penser que, dans un espace-temps vide, il y a un seul point privilégié par rapport à l'autre? Non, donc l'espace-temps vide est homogène.

Est-il raisonnable de penser que, dans un espace-temps vide, une seule direction est privilégiée par rapport aux autres? Non, donc l'espace-temps est également isotrope.

À partir de ces deux hypothèses, Feigenbaum montre l'existence d'une vitesse limite. D'un autre côté, il est également intéressant de noter que dans la théorie d'Einstein, l'existence d'une vitesse limite est un axiome. Cependant, cela est, dans un certain sens, inutile. En effet, en supposant moins de choses (comme seulement l'homogénéité et l'isotropie), on peut montrer qu'il doit exister une vitesse limite.

Maintenant, le fait que CETTE vitesse limite est la vitesse de la lumière, c'est une question que Feigenbaum la théorie ne montre ni ne prouve. Ce fait doit être corrigé par une expérience!

Dernière mise en garde

Que reste-t-il vraiment vrai dans un espace-temps plein de matière? Tout ce que j'ai écrit ci-dessus fonctionne toujours et est valide, mais seulement localement , à savoir dans de très petites zones de l'espace-temps, et zone par zone.

Globalement, cela n'a aucune signification à indiquer / disons qu'il existe une vitesse limite (parce que le concept lui-même d'une vitesse globale est mal défini) et il peut arriver que parfois se déplace avec une vitesse supra-luminale. Par exemple: les galaxies lointaines s'éloignent de nous avec des vitesses bien supérieures à la vitesse de la lumière.

Il n'est pas particulièrement inhabituel pour les systèmes physiques d'avoir des limites de vitesse.

Considérons la corde élastique vibrante classique, définie par l'équation

$$ \ frac {\ partial ^ 2 } {\ partial t ^ 2} \, y (x, t) = -a \ frac {\ partial ^ 2} {\ partial x ^ 2} \, y (x, t) $$

En utilisant cette équation, vous pouvez voir qu'une petite perturbation dans une partie de la corde se propage vers l'extérieur à une vitesse particulière. En fait, vous verrez que la vitesse à laquelle toute perturbation peut se déplacer le long de la chaîne est limitée par cette vitesse.

Vous pouvez donner un sens intuitif à cette vitesse en imaginant que la chaîne est constitué de petites perles reliées par des fils élastiques, et le signal doit se propager en passant de perle en perle, ce qui limite sa vitesse.

Vous verrez un phénomène similaire dans les équations différentielles pour un élastique 3D solide (comme un cube de jello). Également les équations différentielles pour un signal électrique dans un fil, ou une onde électromagnétique dans l'espace, ou une onde sonore dans l'air.

À peu près tout système qui peut être décrit par une équation différentielle qui relie le taux du changement au fil du temps vers une propriété locale comme le dérivé ou la densité finira par avoir une limite de vitesse. Et il est assez courant que les systèmes physiques se comportent de cette façon, car la plupart des choses dans le monde sont constituées de parties plus petites, et le comportement macroscopique du système peut être analysé en termes de comportement des plus petites parties.

Je me rends compte que cela ne répond pas du tout à pourquoi . Je veux juste souligner que le fait d'avoir une limite de vitesse n'est pas une chose aussi inhabituelle ou surprenante.

Pour le dire simplement, c'est la manière de la nature de préserver la causalité .Depuis Wikipédia:

"D'un autre côté, si les signaux pouvaient se déplacer plus vite que la vitesse de la lumière, cela violerait la causalité car cela permettrait d'envoyer un signal à travers des intervalles semblables à des espaces, ce qui signifie qu'au moins pour certains observateurs inertiels, le signal se déplaceraiten arrière dans le temps. Pour cette raison, la relativité restreinte ne permet pas une communication plus rapide que la vitesse de la lumière. "

S'il n'y avait pas de limite de vitesse, toute sorte de paradoxe impliquant une violation de la causalité serait possible (peut-être avez-vous entendu parler du paradoxe du grand-père?).

Une réponse physique:

Lorsqu'un corps chargé électriquement se déplace par rapport à un observateur, un champ magnétique induit peut être mesuré par l'observateur.L'énergie stockée dans ce champ magnétique tend vers l'infini tandis que la vitesse du mobile se rapproche de c.

Une certaine constante c aux dimensions d'une vitesse est nécessaire car les boosters ne commutent pas, et donc les boosters doivent être effectués par des radians sans dimension (mathématiques). La constante c convertit les vitesses en radians. La constante c ne peut pas être infinie car cela ferait basculer les boosts.

Donner à un objet une vitesse (booster) dans la direction x ne commute pas avec un boost dans la direction y. Les augmentations et les rotations obéissent empiriquement à la définition d'un groupe. La relativité restreinte a découvert que les boosters sont des membres du groupe non abélien de Lorentz. Pour $ \ frac {v} {c} \ ll 1 $ il est vrai que

$$ \ operatorname {Boost} {\ left (\ frac {v_x} {c} \ right)} \, \ operatorname {Boost} {\ left (\ frac {v_y} {c} \ right)} - ​​\ operatorname {Boost} {\ left (\ frac {v_y} {c} \ right)} \, \ operatorname {Boost} {\ left (\ frac {v_x} {c} \ right)} = \ operatorname {Rotation} _ {z} {\ left (\ frac {v_x} {c} \ frac {v_y} {c} \ right)} \,. $$

Il doit y avoir une constante $ c $ avec des dimensions de vitesse pour rendre les paramètres de boost sans dimension radians afin que leur produit (l'angle de rotation autour de l'axe $ z $) puisse également être en radians sans dimension. Il est normal que $ radians ^ 2 = radians $ comme en témoignent les termes de l'expansion de la série de puissance de $ \ sin {\ left (\ theta \ right)} $. Il est absurde de faire une rotation autour de l'axe $ z $ par $ {\ left (\ frac {\ mathrm {m}} {\ mathrm {s}} \ right)} ^ {2} $.

Si $ c \ à \ infty $, alors les boosts feraient la navette, et ils ne feraient plus partie du groupe Lorentz. La constante c est similaire à la constante $ a = {\ left (\ frac {180} {\ pi} \ right)} \, \ mathrm {degrés} $ qui est utilisée pour convertir les angles $ \ Theta $ de degrés en radians . Le groupe de rotation (qui est un sous-groupe du groupe de Lorentz) n'est pas abélien

$$ \ small {\ operatorname {Rotation} {\ left (\ frac {\ Theta_x} {a} \ right)} \, \ operatorname {Rotation} {\ left (\ frac {\ Theta_y} {a} \ right)} - ​​\ operatorname {Rotation} {\ left (\ frac {\ Theta_y} {a} \ right)} \, \ operatorname {Rotation} {\ left (\ frac {\ Theta_x} {a} \ right)} = \ operatorname {Rotation} _z {\ left (\ frac {\ Theta_x} {a} \ frac {\ Theta_y} {a} \ right)}} \,. $$

Le "$ a $ " est nécessaire. Il serait absurde de faire une rotation autour de l'axe $ z $ de $ \ left [\ text {degrés} \ right] ^ 2 $. Si $ a \ à \ infty, $ alors les rotations feraient la navette, et elles ne feraient plus partie du groupe de Lorentz. Si les rotations faisaient la navette, notre monde serait très différent. Il n'y aurait rien de tel que de faire pivoter un objet d'un angle différent de zéro et de le faire revenir à son orientation d'origine. De plus, le moment cinétique ne serait pas quantifié et les particules n'auraient pas de spin.

En résumé, c (et a) sont nécessaires et doivent être finis car les accélérations (et les rotations) font partie du Lorentz non abélien groupe. Ce groupe est d'où vient le paramètre de boost $ \ left [\ text {rapidity} \ right] = \ tanh ^ {- 1} {\ left (\ frac {v} {c} \ right)} $ dans la réponse de Kostya.

En GR, la vitesse de la lumière n'est pas constante, elle varie avec la courbure de l'espace-temps. Ainsi, la constance de cette vitesse universelle dépend de l'espace - le temps a une courbure constante. Ce qui n'est pas le cas, mais c'est localement une approximation utile, et afin de répondre à l'intention de l'OP, nous supposerons désormais que l'Univers est un espace de courbure constante.Dans tous les cas, nous savons que la vitesse de la lumière est plus lent lorsque la courbure est plus grande, donc si nous recherchons la limite, nous devons considérer le cas de la courbure nulle constante, car partout ailleurs elle sera plus lente.

Maintenant, pour simplifier, supposons cette courbure est zéro.

On observe expérimentalement que la masse est équivalente à l'énergie, donc ils ont les mêmes unités. Mais la masse supplémentaire produite par l'énergie cinétique d'une ville v est $ {1 \ sur 2} m v ^ 2 $ donc v doit être sans dimension. Par conséquent, il existe un système de coordonnées pour l'espace-temps dans lequel les coordonnées x ont les mêmes unités que les coordonnées t. Puisque la variété est complètement plate, pratiquement euclidienne (sauf pour le -1 dans la signature de la métrique), on peut choisir un système de coordonnées qui est, naïvement parlant, le même partout. Ainsi, une direction semblable à un espace peut être tournée vers une direction semblable au temps de la même manière, uniformément, partout. (Cela peut ressembler à SR, mais ce n'est pas encore SR. Il s'agit simplement d'une analyse dimensionnelle plus une géométrie simple plus ce fait expérimental de l'équivalence de la masse avec l'énergie). Mais alors nous avons une vitesse universelle, cette même conversion entre la coordonnée x et la coordonnée t.

Jusqu'à présent, cela ne dit pas que la vitesse est une limite de vitesse, ni que cela a à voir avec la lumière. Mais il est canonique et intrinsèque et "physique" car il dépend du rapport de conversion entre masse et énergie.

L'étape suivante consiste à déduire qu'il s'agit d'une limite de vitesse universelle. Cela se fait comme d'habitude, car l'accélération augmente la masse de l'objet et donc un "rendement décroissant" exactement quantitatif s'applique.

Donc, tout ce que nous voulons découle de la relation de Newton entre la masse, l'énergie cinétique et la vitesse, plus le seul fait expérimental de l'équivalence masse-énergie.

Note: William Davidon a publié quelque part un note montrant comment tout SR découle de l'équivalence masse-énergie. Je ne l'ai pas lu, mais le simple fait d'entendre le fait qu'il l'a fait m'a évidemment permis de comprendre cela. Il faut donc reconnaître cette «priorité».

Il ne peut y avoir de raison philosophique très fondamentale pour laquelle la masse doit être équivalente à l'énergie, puisque la physique théorique est possible dans une voie galiléenne, là où elle n'est pas vraie. D'un autre côté, philosophiquement, on pourrait toujours considérer le cas galiléen comme inclus dans ce cadre en ce sens que $ \ infty $ est une constante universelle et une limite de vitesse universelle, aussi, avec des droits égaux à 1. (Il vaut zéro comme une limite de vitesse universelle qui ne pourrait jamais être acceptée en physique ... pas même en théorie.)

J'ai remarqué que plus on se rapproche des théories physiques fondamentales, celles qui décrivent les interactions les plus élémentaires de notre univers, plus les équations commencent toutes à ressembler à des transformations de coordonnées. Parfois, ces coordonnées sont dans des espaces abstraits - les groupes du modèle standard de la physique des particules et les espaces de Hilbert de la mécanique quantique - mais, finalement, la physique est une description du mouvement des choses.

Afin de localiser quelque chose dans l'univers, vous avez besoin à la fois de position et de temps. Maintenant, même si vous restez assis en lisant ceci, vous avancez dans le temps. La vitesse à laquelle vous vous déplacez dans le temps est d'une seconde par seconde selon votre propre montre, mais tout le monde ne sera pas d'accord avec cela. Voyons à quelle vitesse vous allez selon n'importe quel observateur.

Permet de vous envoyer en voyage vers le système stellaire Alpha Centauri à une grande fraction de la vitesse de la lumière. Un résident de votre destination observe votre voyage et constate que vous avez parcouru une distance de $ d $ (environ 4 années-lumière). Selon la montre que vous portez, vous avez vieilli d'un temps $ t $, ce qui est inférieur au temps pendant lequel l'Alpha Centaurian a mesuré votre voyage dû à la dilatation du temps. Pour trouver votre voyage total dans l'espace-temps, nous pouvons combiner votre voyage en deux dimensions avec le théorème de Pythagore: $$ x = \ sqrt {d ^ 2 + t ^ 2}. $$ La distance totale que vous avez parcourue dans l'espace et le temps est de $ x $; la distance que vous avez parcourue dans l'espace est de $ d $; et la distance que vous avez parcourue dans le temps est $ t $ (ce qui équivaut à dire combien vous avez vieilli). Le problème avec cette équation est que $ d $ et $ t $ sont dans des unités différentes: mètres et secondes. Heureusement, la relativité d'Einstein fournit un facteur de conversion: la vitesse de la lumière. Donc, l'équation doit lire: $$ x = \ sqrt {d ^ 2 + {\ left (ct \ right)} ^ 2}. $$

Maintenant, la distance que vous avez parcourue est égale à la vitesse du vaisseau spatial multipliée par le temps du voyage mesuré par l'Alpha Centurion (la distance mesurée dans le cadre de repos de deux points est appelée distance appropriée . L'heure correcte est mesurée par une horloge au repos avec l'entité chronométrée, à savoir votre montre.). Appelons le temps écoulé dans Alpha Centauri $ t_ \ alpha $. $$ x = \ sqrt {{\ left (vt_ \ alpha \ right)} ^ 2 + {\ left (ct \ right)} ^ 2}. $$ On peut relier $ t $ et $ t_ \ alpha $ à l'équation de dilatation du temps: $$ t = \ frac {t_ \ alpha} {\ gamma} = t_ \ alpha \ sqrt {1 - {\ left (\ frac {v } {c} \ right)} ^ 2} $$ où $ \ gamma $ est le facteur relativiste qui apparaît dans presque toutes les équations relativistes. Notez que $ t_ \ alpha $ est plus petit que $ t $ pour refléter le vieillissement plus lent que subissent les objets en mouvement rapide (vous).

Donc, maintenant, nous avons $$ x = \ sqrt {{\ left (vt_ \ alpha \ right)} ^ 2 + \ left (ct_ \ alpha \ sqrt {1- \ left (\ frac {v} {c} \ right) ^ 2} \ right) ^ 2}. $$ Simplification: $$ \ begin {align} x & = \ sqrt {v ^ 2t_ \ alpha ^ 2 + c ^ 2t_ \ alpha ^ 2 \ left (1- \ left (\ frac {v} {c} \ right) ^ 2 \ droite)} \\ [5px] & = t_ \ alpha \ sqrt {v ^ 2 + c ^ 2 \ gauche (1- \ gauche (\ frac {v} {c} \ droite) ^ 2 \ droite)} \\ [5px] & = t_ \ alpha \ sqrt {v ^ 2 + c ^ 2 - v ^ 2} \\ [5px] & = t_ \ alpha \ sqrt {c ^ 2} \\ [5px] & = ct_ \ alpha \,. \ end {align} $$ La distance totale que vous avez parcourue dans l'espace et dans le temps est égale à la vitesse de la lumière multipliée par votre temps de trajet. Cela est vrai quelle que soit votre vitesse. Ainsi, lorsque vous prenez votre mouvement à travers l'espace et le temps ensemble, vous vous déplacez toujours à la vitesse de la lumière! Penser que différents objets voyagent à des vitesses différentes ignore leur mouvement dans le temps. Ainsi, la vitesse de la lumière n'est pas seulement une vitesse maximale. C'est aussi une vitesse minimale. On pourrait dire que c'est la seule vitesse.

Une conséquence de ceci est que plus vous vous déplacez rapidement dans l'espace, plus vous vous déplacez lentement dans le temps et vice versa. Vous pouvez imaginer cette situation comme si vous conduisiez dans une voiture sans pédale d'accélérateur et sans pédale de frein - juste un volant. Il se déplace toujours à la même vitesse. Si vous voulez rouler vers l'est, vous devez sacrifier une certaine vitesse vers le nord. De la même manière, si vous voulez vous déplacer dans l'espace, vous devez sacrifier une certaine vitesse dans le temps. En fait, le calcul fonctionne de la même manière pour la relativité si vous imaginez un axe comme espace et l'autre comme temps comme je l'ai fait dans la dérivation ci-dessus.

Maintenant, y a-t-il une raison fondamentale de répondre pourquoi c'est ainsi? Le mieux que je puisse trouver est d'observer que nous n'avons aucun contrôle sur la vitesse à laquelle nous vieillissons. Un an pour vous est exactement la même année pour moi (à moins qu'un vaisseau spatial avancé ne soit bientôt inventé). Si le temps n'est pas si différent de l'espace, comme il semble l'être dans notre univers, alors, comme le temps, le voyage dans l'espace serait également limité à une certaine vitesse. Le fait fondamental de notre univers qui fixe la vitesse limite de la lumière est l'interdépendance du mouvement à travers l'espace et le temps.

La question dans l'en-tête était

Savons-nous pourquoi il y a une limite de vitesse dans notre univers? »

Puis il y a eu une amplification

Cette question est de savoir pourquoi nous avons une limite de vitesse universelle (la vitesse de la lumière dans le vide). Existe-t-il une loi plus fondamentale qui nous explique pourquoi? Je ne demande pas pourquoi la limite de vitesse est égale à c et pas autre chose, mais pourquoi il y a une limite du tout.

Je pense que de toutes les réponses, @Anna_v s'est rapprochée pour répondre à la question.

À l'heure actuelle, la réponse à la question est «Non».

L ' idée qu'il y a une limite de vitesse universelle vient des observations de l'Univers.
Ces observations aboutissent à certaines théories qui peuvent être utilisées pour faire des prédictions sur l'Univers.
Un certain nombre de ces théories qui sont bonnes pour faire des prédictions ont l ' idée qu'il existe une limite de vitesse universelle.
En d'autres termes, la limite de vitesse universelle est un postulat utile car elle fait certaines des théories «fonctionnent».
Les théories actuelles ne sont pas capables de prédire tout ce qui s'est passé et se produira et les scientifiques recherchent donc de meilleures théories.

Existe-t-il une théorie qui expliquera pourquoi il y a une limite de vitesse universelle est inconnue.

À l'heure actuelle, une telle théorie n'existe pas.

OK, nous parlons de vitesse et du fait qu'il y a une limite à la vitesse. On parle donc de mouvement. Le mouvement contient deux variables. L'un est la vitesse et l'autre la distance. Les variables vont de zéro à l'infini. Ainsi, pour regarder la plus grande image possible concernant le mouvement, on pousserait naturellement ces deux variables à l'infini.

Voyager à une "vitesse" infinie signifie parcourir n'importe quelle distance, en un temps nul. Cela signifie que l'on peut voyager du point A au point B en disons 1 minute, mais cela signifie également que vous pouvez voyager plus vite et terminer le voyage en moins d'une seconde. Plus vous allez vite, moins vous avez besoin de temps. Ce sont des vitesses finies. Mais si vous voyagez du point A au point B en un rien de temps, il n'y a aucun moyen de battre cette vitesse particulière. C'est la vitesse infinie.

Suivant. Traverser une «distance» infinie signifie que vous continuerez indéfiniment puisqu'il n'y a pas de fin à une distance infinie. Ainsi, si vous combinez les deux et parcourez une distance infinie à une vitesse infinie, cela signifie que vous allez go sur pour toujours, en un rien de temps du tout. De manière holistique, ce n'est tout simplement pas possible. Cependant, relativistiquement, c'est possible, et c'est possible puisque les deux extrêmes se séparent.

Dans un extrême possible, vous pouvez vous déplacer dans l'espace mais ne vous déplacerez pas dans le temps. Dans l'autre extrême possible, vous vous déplacerez dans le temps mais pas dans l'espace. Pour rendre cette transition possible, si vous gagnez dans l'un, vous devez perdre dans l'autre. Ainsi, vous ne pouvez pas avoir les deux extrêmes en même temps. Ainsi, ils doivent à leur tour être englobés dans un fini pour provoquer ce phénomène de gain et de perte.

En retour, vous pouvez vous déplacer dans l'espace mais pas dans le temps, tandis que pour ceux qui vous observent, le temps passe toujours pour eux, et donc même si le temps est au point mort pour vous, le temps peut s'éterniser, ailleurs. Ainsi, vous pouvez continuer indéfiniment, en un rien de temps.

Ainsi, le mouvement fini à travers l'espace-temps est une exigence pour rendre le mouvement possible.Il y a donc une limite finie à la vitesse du mouvement dans l'espace.

Si vous analysez ensuite le résultat de ce phénomène, vous découvrez indépendamment la Relativité Spéciale et dérivez indépendamment toutes ses équations mathématiques.Regardez cette vidéo pour vérification.

Pourquoi y a-t-il une limite de vitesse dans notre univers?Cela pourrait avoir quelque chose à voir avec le principe de localité en physique.Notez que dans l'univers de Fredkin en tant qu'automate cellulaire, il y a toujours une limite de vitesse, pour tout schéma émergent (juste un exemple).Ainsi, l'existence d'une limite de vitesse dans notre univers est une approbation (conséquence) du principe de localité en physique.En passant, les arguments de non-localité quantique (basés sur des expériences d'intrication quantique) doivent être expliqués en termes de systèmes chaotiques synchronisés, mais sans rejeter le principe de localité.

Le point de départ de l'argument d'Einstein était que les coordonnées spatio-temporelles ne sont pas un préalable physique, mais sont établies à partir des procédures de mesure physique. Si nous supposons le principe général de la relativité

• Les lois locales de la physique sont les mêmes quelle que soit la matière de référence utilisée par un observateur particulier pour les quantifier

alors tous les observateurs définissent les coordonnées de la même manière, ce qui signifie qu'une vitesse maximale (s'il y en a une) sera la même pour tous les observateurs. Soit il y a, soit il n'y a pas de vitesse maximale dans la nature. En écartant l'argument selon lequel l'absence de vitesse maximale contredit l'observation, nous pouvons observer que tous les processus physiques prennent du temps. L'absence de vitesse maximale impliquerait la possibilité d'une action instantanée à distance (au moins dans une limite), ce que Newton a décrit comme

une si grande absurdité que je crois qu'aucun homme qui a en matière philosophique une faculté de pensée compétente ne pourra jamais y tomber .

La quantité de masse d'un objet = la résistance au changement d'élan de cet objet.Plus il y a de masse, plus il faut d'énergie pour changer d'élan.Puisque les photons sont sans masse, ils n'ont aucune résistance aux changements d'impulsion.Les photons sont essentiellement la vitesse à laquelle l'énergie se propage dans l'univers.Quant à savoir pourquoi c'est c, c'est comme ça que l'univers se déroule.Il n'y a pas de loi selon laquelle quelque chose ne peut pas bouger plus vite, mais si nous considérons le monde physique comme la dualité énergie / masse, alors rien de physique ne peut aller plus vite que la lumière.

La raison pour laquelle il y a une limite de vitesse dans notre Univers, c'est que nous n'avons rien (pas d'énergie / force) qui puisse nous aider à déplacer quelque chose plus vite que la vitesse la plus élevée qui nous est disponible $ \ left (c \ right) $.

En d'autres termes, si la vitesse de $ c $ était de 2 $ {\ cdot} {10} ^ {8} \ frac {\ mathrm {m}} {\ mathrm {s}} $ (ou 4 $ {\ cdot} {10} ^ {8} \ frac {\ mathrm {m}} {\ mathrm {s}} $), alors this serait la limite de vitesse de l'Univers.Le mieux que nous puissions faire serait de donner à match la vitesse de $ c $.

La lumière voyage le plus rapidement dans l'univers en raison de sa vitesse mais aussi en raison de sa trajectoire.Pierre de Fermat a soutenu que "la lumière se déplace entre deux points le long du chemin le plus court".Cela peut être appelé le principe du moindre temps.Ensuite, il y a le principe de la moindre action.Citant Pierre Louis Maupertuis "la nature est économe dans toutes ses actions".Pouvez-vous penser à un exemple dans la nature où les ressources / l'énergie sont gaspillées?Je suggérerais prudemment que la nature n'a pas besoin d'un mouvement plus rapide que la lumière et ne l'a donc pas fourni.

La vitesse de la lumière s'applique à plus que la simple lumière, rien ne peut se propager plus rapidement, y compris les forces qui agissent sur la matière. Il existe cependant une réponse non traditionnelle pour expliquer pourquoi. La vitesse de la lumière est une vitesse maximale car nous voyageons tous dans un milieu porteur d'onde, l'espace-temps. La lumière, comme une onde dans le milieu, s'y déplace à une vitesse constante; et comme tout le reste dans un voyage en douceur dans un "fluide", nous nous déplaçons plus lentement qu'une onde voyageant dans le fluide de l'espace-temps, comme observé avec des objets dans l'eau ou dans l'air ou des vagues dans des solides. (Les solides sont un cas particulier, car seules les ondes les traversent.)

L'analogie laisse entendre qu'il n'y a peut-être pas de limite de vitesse absolue , mais tout ce que nous avons observé traverse le «fluide» de l'espace-temps et ne peut pas être utilisé pour accélérer au-delà de la vitesse de la lumière, donc nous sommes coincés. Il existe classiquement deux cas d'accélération.

1) La chose qui accélère a de la masse:

Nous avons observé que la masse, telle qu'observée par un observateur externe, varie sous la forme d'un rapport de $$ \ frac {1} {\ sqrt {1 - v ^ 2 / c ^ 2}} $$ Donc, notre observation dit que la masse va à l'infini à mesure que v s'approche de c , mais nous ne savons pas «pourquoi» exactement, mais cela agit comme une résistance croissante au voyage par un «moyen» ou des rendements décroissants essayant d'ajouter de l'élan à l'objet en déplacement. En fonction de l'énergie requise pour augmenter la vitesse, votre rendement en augmentation de vitesse diminue de moins en moins parce que la résistance au mouvement, la «masse», devient de plus en plus grande et finalement, à cause de la «masse», l'énergie (qui est des vagues ou de la matière sur le même support que l'objet que nous accélérons, donc il doit voyager plus lentement que la vitesse de la lumière) devient finalement si inefficace qu'il ne cause pas vraiment d'effet pour aucune source d'énergie connue.

2) La chose qui accélère n'a pas de masse:

La seule chose que nous connaissons actuellement qui n'a pas de masse, mais qui est mesurable d'une certaine manière est une chose vague / particule, et elle ne peut pas accélérer, elle voyage simplement à travers le fluide de l'espace-temps.La gravité, EM comme la lumière, les forces fondamentales se propagent toutes sous forme d'onde sur un média.Et encore une fois, ce média est "Spacetime" mais nous ne savons pas de quoi il est fait.D'autres ondes voyagent à travers la matière et il y a une vitesse d'onde mesurable dans chacune d'elles.MAIS, c'est un voyage dans la matière, dans l'espace-temps.

3) Le troisième cas d'accélération de la matière au-delà de la vitesse de la lumière est une spéculation intéressante, mais finalement futile, car ce n'est pas possible selon la physique connue car il n'y a aucun moyen d'ajouter plus d'élan après avoir atteint la vitesse de la lumière.Si quelqu'un ajoutait une force qui poussait sur autre chose que "l'espace ...", il y aurait une expérience de pensée pour un voyage plus rapide que les vagues au milieu de l'espace-temps.

Si vous regardez plus vite que le réveil dans un autre support, vous pouvez voir que c'est possible, mais les choses changent. Pendant un moment, nous avons pensé que nous ne pouvions pas voyager plus vite que le son, mais comme il n'y a pas de limite d'accélération, quelque chose de spécial se produit à la frontière, un avion peut la dépasser et cela provoque une onde de choc conique derrière lui. Un bateau peut voyager plus vite que les vagues dans l'eau, et là encore, une vague déferlante, une «onde de choc» apparaît à la surface derrière le bateau. Que signifierait accélérer pour voyager plus vite que les vagues voyageant dans l'espace-temps? Nous ne pensons pas que cela puisse être fait, mais il semble que nous sachions en quelque sorte à quoi cela pourrait ressembler avec un voyage relativiste FTW à vitesse plus lente. Il y a un nom pour l'onde de choc créée lorsque la matière se déplace plus rapidement que la vitesse locale de la lumière (un réacteur à fission est l'exemple habituel), appelé rayonnement Tchérenkov, qui suit avec la normale plus rapidement que le déplacement des ondes dans un fluide. (Nous voyons de la lumière visible, une jolie nuance de bleu.) Pour voyager dans des fluides normaux, voyager plus vite qu'une vague provoque un nouveau régime de sillage. Avec la vitesse de la lumière, la vitesse d'une onde dans l'espace-temps, pourrait-il en être de même? Peut-être, s'il y avait une autre force, une autre façon d'ajouter de l'élan au système. Quelque chose se déplaçant plus vite que c pourrait potentiellement former une onde de choc et peut-être déformer l'espace-temps d'une nouvelle manière. Il y a des indices que l'espace-temps agit comme un fluide compressible en masse; Si vous excluez la gravité en tant que force pouvant agir directement sur la lumière, la lumière qui se courbe autour d'une masse suffisamment grande ressemble à ce qui se passe lorsque la vitesse d'un objet change dans la direction perpendiculaire à son déplacement, ce que nous appelons la réfraction. C'est probablement une comparaison erronée, cependant, car il n'y a aucune preuve que la lumière PEUT accélérer; autrement, l'horizon des événements autour d'un trou noir n'absorberait pas la lumière. Mais il y a des gens qui s'intéressent à la densité de l'espace. Donc, il y a des recherches sur les bords, mais dépassant cette limite de c Pas si probable, mais intéressant à considérer.

Je ne suis pas d'accord sur le fait qu'il existe une limite de vitesse universelle dans notre univers, à moins bien sûr que vous ne définissiez le mot «vitesse» d'une manière très peu intuitive.

Je prétends que diviser la longueur appropriée de la distance parcourue dans le cadre de l'observateur par le temps propre dans le cadre de l'objet $ \ left (= \ gamma \ cdot v \ right) $ est plus proche de notre compréhension intuitive de la vitesse que la variable $v $ (qui est défini par rapport à la définition peu intuitive du temps en relativité restreinte).Cette quantité n'est pas limitée à $ c $.

De manière équivalente, on peut prendre la grandeur du vecteur constitué uniquement des composantes spatiales des quatre vitesses.Encore une fois, ce n'est pas égal à $ v $ et peut être supérieur à $ c $.

théorie de Tachyon pourrait apporter quelques éclairages sur cette question. Selon la théorie des tachyons, il est possible qu'une particule puisse voyager plus vite que la vitesse de la lumière tant que la particule a été créée avec une vitesse supérieure à la vitesse de la lumière. Et la vitesse de la frontière de la lumière, selon la théorie des tachyons, peut être approchée par le bas ou par le haut, mais pas être franchie. Un tachyon à vitesse infinie n'aura aucune énergie relativiste, mais gagnera de l'énergie en décélérant vers la vitesse de la limite de la lumière.

$ \ hspace {100px} $

Mais des vitesses aussi rapides que la lumière ont d'étranges propriétés temporelles, les particules voyagent si vite qu'elles remontent constamment dans le temps et viendront toujours du futur et remonteront dans le passé. Vu de notre réalité, cela pourrait être considéré comme des particules voyageant constamment vers des trous de ver vers le passé, et nous n'avons jamais observé de telles particules, et il pourrait même ne pas être possible d'observer de telles particules.

Le lien quantique a été mesuré en utilisant des lasers et l'intrication quantique comme étant au moins 10 000 fois plus rapide que la lumière, donc il a une vitesse infinie ou proche de la vitesse infinie. Einstein n'aimait pas l'intrication quantique, car cela semble briser sa limite de vitesse à la lumière. Nous ne savons pas exactement quel est le lien quantique, certains suggèrent des trous de ver, certains suggèrent une superposition, certains disent qu'il est lié sur un plan fondamental, des ondes sans particules, etc., mais si le lien quantique implique des particules en déplacement, ces particules doivent être tachyons particules à vitesse infinie ou proche de l'infini.

Et il est étrange qu'en mécanique quantique, l'observateur puisse influencer le résultat d'une expérience. Le résultat de l'expérience est remonté dans le temps car il faut quelques nanosecondes avant que la lumière ne nous atteigne afin que nous puissions observer le résultat de l'expérience. Comme l'observation influence un résultat, est-ce que l'observation ressemble à la sélection des potentiels quantiques passés du futur? Et relativement parlant, l'expérience a-t-elle vraiment eu lieu dans le passé? Ces choses me déroutent souvent.

Richard Feynman et Wheeler avaient une étrange hypothèse, que se passerait-il si la lumière était émise par un photon avancé qui voyageait dans le temps et émettait la lumière. Nous pourrions soutenir que cela ne rompt pas la causalité, car le temps linéaire de cette particule va dans l'autre sens. Cette réponse de Terry Bollinger explique magnifiquement cette hypothèse: Un photon peut-il être émis sans récepteur?

Inspiré par Feynman, je me demande s'il y a une relation ici, si un tachyon avec une vitesse proche de l'infini et une énergie proche de zéro est émis, de notre œil au même moment où une lumière est reçue, le tachyon pourrait temps à l'émetteur et influencer le saut quantique qui a émis la lumière? La relation est alors: la vitesse infinie correspond-elle à la vitesse de la lumière en sens inverse? Quelqu'un sait comment calculer cela?

S'il existe une telle relation, nous pourrions nous demander si la vitesse infinie joue un rôle dans la définition de la vitesse de la limite de la lumière.