Vous n'obtenez pas de réponse dans un monde idéal. C'est la frontière entre 2 résultats différents. La réponse dépend des détails qui ont été idéalisés.

Lorsqu'une balle touche un obstacle, elle se déforme. De même, la paroi est au moins un peu déformée par la balle. Ces changements de forme n'ont pas beaucoup d'importance pour les deux premiers cas, mais ils peuvent avoir un impact plus important dans le scénario suivant;

Supposons que la balle s'écrase horizontalement et devienne plus haute. Cela aura tendance à soulever la balle. De plus, la balle rebondira à mesure qu'elle reprendra sa forme.

--- Modifier

En réponse à Lamar Latrell et Graham, je voudrais faire un point auquel divers commentaires et réponses ont fait allusion. Les deux premiers cas ont des comportements différents.

Lorsqu'une balle rebondit sur le mur, l'interaction se déroule sur un temps très court. La force est très grande. La balle se déforme et ressort assez fort pour voler du mur. Dans le cas d'une collision élastique, il ressort avec la même vitesse. Ceci est souvent ignoré lorsque les gens ne s'intéressent qu'à la vitesse finale. Il est abstrait comme une collision instantanée.

Lorsqu'une balle glisse sur une courbe douce, l'interaction prend beaucoup plus de temps. Les forces sont relativement douces et la déformation est moindre. Le retour de ressort est d'environ $ 0 $ . Les forces normales du mur ralentissent la balle et la soulèvent.

Lorsque le rayon du coin est légèrement plus grand que la balle, les déformations deviennent importantes. Le point de contact peut se déplacer rapidement du bas vers le côté. Mais il peut également passer d'un point à un patch. Il faut penser en 3 dimensions. Une sphère enroule un cylindre. Le patch a une surface, pas seulement une longueur.

Lorsque les rayons correspondent, le point de contact devient définitivement un patch d'au moins 90 degrés. Il s'aplatit également sur le mur.

Les forces dépendent du degré d'aplatissement.Certaines forces seront à la hausse.Cela dépend de détails comme la forme du patch.Ceci est contrôlé par les propriétés de la balle.

Dans un monde idéal, la balle est considérée comme infiniment rigide.Dans ce cas, vous pouvez appliquer des forces normales le long d'une ligne de contact en même temps comme AccidentalTaylorExpansion et d'autres l'ont fait (+1).Mais vous ne devriez pas être surpris si un meilleur modèle de l'interaction donne une réponse différente.En particulier, les forces normales ne font pas directement voler la balle du mur.Ils provoquent une déformation et les forces internes de la balle la font revenir en forme et s'envoler.

Si vous voulez vous compliquer la vie, asseyez-vous et attachez-vous parce que je vais à fond.

Tout d'abord, nous devons regarder comment la balle rebondit en premier lieu, car c'est plutôt délicat pour les rebonds instantanés. Considérez la situation suivante:

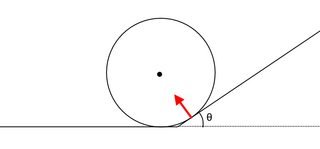
Une balle avec un élan initial $ \ vec p $ se déplace vers la droite et touche une pente. Ignorons la gravité pour l'instant car ce problème va être assez compliqué. Pendant la collision, une force agira sur le ballon et nous ne savons pas exactement à quoi ressemble cette force, mais nous savons deux choses

1. La force est une force normale, donc lors de la collision, la force sera le long d'une ligne joignant le point de contact et le centre de la balle (voir la flèche rouge sur l'image)
2. L'énergie sera conservée (environnement idéal) donc $ | \ vec {p} \, '| = | \ vec p | $ où $ \ vec p \, '$ est l'élan après la collision.

À partir de là, nous pouvons conclure que la dynamique changera de la manière suivante:

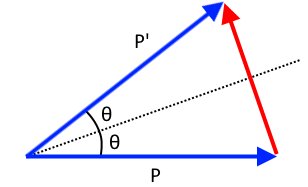
L'élan est tourné par $ 2 \ theta $ depuis $ \ Delta p $ , la flèche rouge , doit être parallèle à la force normale. Maintenant, appliquez ceci aux deux cas de bord que vous avez mentionnés pour voir que cela a du sens. Pour la collision frontale, nous avons $ \ theta = \ pi / 2 $ donc l'élan sera tourné par $ \ pi $ . Cela signifie que la particule rebondira directement comme prévu. Pour le cas avec le grand arc, nous avons une courbe variant continuellement. Décomposons la courbe en plusieurs segments de ligne et prenons la limite vers une courbe continue. Dans cette limite, l'angle entre deux sections passe à zéro, de sorte que l'angle auquel la balle rebondit va également à zéro. La balle continue à épouser la courbe comme prévu.

Regardons maintenant le cas où le rayon de courbure est égal au rayon de la balle. Cette affaire est délicate et nous devons faire des choix. Considérons un court intervalle de temps pendant lequel la collision se produit. Tout le quart inférieur droit de la balle subit une force en même temps, mais nous ne savons pas vraiment comment cette force est répartie. Je vais faire l'hypothèse suivante pour que nous puissions réellement calculer quelque chose: la force à chaque point de contact est proportionnelle à $ \ hat r \ cdot \ vec v $ , où $ \ vec r $ est le vecteur joignant le centre de la balle et le point de contact et $ \ hat r = \ tfrac 1 r \ vec r $ . La force est également dans la direction de $ \ hat r $ car c'est une force normale. Convainquez-vous que cela correspond au cas que j'ai mentionné en premier. Je définis $ \ phi $ de sorte que $ \ phi = 0 $ au point de contact le plus à droite et $ \ phi = \ pi / 2 $ au point de contact le plus bas.

Le changement total de moment peut maintenant être écrit comme une intégrale sur tous les angles de contact ( $ \ phi $ ). Puisque nous ne connaissons pas encore l'ampleur exacte, j'introduis un facteur $ c $ à déterminer plus tard. $$ \ Delta \ vec p \ propto \ int (- \ hat r \ cdot \ vec v) \ hat r \ mathrm {d} \ phi \\ = c \ int_0 ^ {\ pi / 2} (- \ cos \ phi) \ begin {pmatrix} \ cos \ phi \\ - \ sin \ phi \ end {pmatrix} \ mathrm {d} {\ phi} \\ = c \ begin {pmatrix} - \ pi / 4 \\ 1/2 \ end {pmatrix} $$ La dernière ligne utilisée $$ \ int_0 ^ {\ pi / 2} - \ cos ^ 2 (\ phi) \, \ mathrm {d} \ phi = - \ pi / 4, \ int_0 ^ {\ pi / 2} \ cos (\ phi) \ sin (\ phi) \, \ mathrm {d} \ phi = 1/2 $$

Pour déterminer $ c $ , j'utilise à nouveau la conversation d'énery. Donc $ | \ vec p + \ Delta \ vec p | = | \ vec p | $ . Brancher cette équation pour $ c $ dans Mathematica donne $$ c = \ frac {8 \ pi mv} {4+ \ pi ^ 2}. $$ Une expression laide, mais au moins une réponse. Le fait qu'il soit proportionnel à $ \ vec p $ rend l'angle toujours le même que vous le verrez bientôt. Pour déterminer l'angle entre deux vecteurs, vous pouvez utiliser $$ \ cos \ theta = \ frac {\ vec a \ cdot \ vec b} {| \ vec a || \ vec b |}. $$ Brancher ceci pour $ \ vec p $ et $ \ vec p \, '= \ vec p + \ Delta \ vec p $ donne enfin (en utilisant à nouveau Mathematica, je ne suis pas fou) $$ \ theta = \ arccos \ left (\ frac {4- \ pi ^ 2} {4+ \ pi ^ 2} \ right) \ approx 115.037 ^ {\ circ} $ $ Ou à propos de cet angle:

Je voudrais souligner à nouveau que j'ai fait des hypothèses sur la façon dont la force est répartie pendant la collision. Votre réponse pourrait donc être différente si vous faites des hypothèses différentes. Vous devez faire ces hypothèses car ce problème est impossible à définir exactement.

TLDR - sous certaines hypothèses, vous pouvez calculer l'angle auquel la particule rebondit. Mes calculs donnent 115 $ ^ {\ circ} $ ( 65 $ ^ {\ circ} $ par rapport au sol)

EDIT - Dans les commentaires, il a été suggéré que la force de restauration pour un angle particulier soit proportionnelle à $ - \ cos ^ 2 \ phi $ au lieu de $ - \ cos \ phi $ . Je ne suis pas entièrement convaincu, mais dans ce cas, le calcul se révèle être $ \ theta = \ arccos (-3/5) \ approx 2,21 $ radians ou 53 $ ^ {\ circ} $ depuis le sol.

La balle remontera la courbe si sa vitesse horizontale n'est pas arrêtée ou inversée. C'est parce que si sa vitesse horizontale devient $ 0 $ , elle ne pourra pas continuer à monter à cause de la gravité. Cela pourrait juste pendant un moment si la vitesse initiale est suffisante.

Premier cas

Ici, comme vous le mentionnez, il ne montera pas car dès qu'il touchera le mur, le ballon recevra une force dans la direction opposée ( en supposant une collision élastique ). De plus, il ne recevra aucune force nette dans le sens vertical car le rayon de courbure du mur est plus petit que celui de la balle.

Deuxième cas

Dans ce cas, la balle se lèvera car c'est une sorte d'inclinaison qui fait varier sa pente. De plus, puisque dans ce cas la balle ne perd pas toute sa vitesse dans la direction $ x $ à la fois, elle peut se déplacer au-dessus de la courbe jusqu'à ce que toute son énergie potentielle soit convertie en énergie cinétique.

Troisième cas

Ici, la balle recevra une force nette qui sera au-dessus du sol dans la direction $ - x $ comme indiqué dans le diagramme. Maintenant, cette force pourrait soulever la balle, mais elle pourrait ne pas être en mesure de le faire à cause de la gravité. S'il n'y avait pas de gravité, la balle remonterait et se dirigerait vers la gauche.

La balle rebondira à un angle initial de 64,96 ° par rapport à l'horizontale.

Au point de contact, la force incidente est répartie sur le quadrant inférieur droit de la balle; une hypothèse raisonnable est que la force incidente (et donc l'impulsion) en un point est proportionnelle au cosinus de l'angle entre la vitesse incidente et la normale à la surface (donc zéro à la base de la balle, s'élevant à sa plus grande valeur au côté droit du ballon). En intégrant et en éliminant les facteurs constants (puisque nous ne nous soucions que de la direction de l'impulsion nette), nous obtenons:

$$ J = \ int_0 ^ {\ pi / 2} \ begin {pmatrix} \ cos ^ 2 \ theta \\ \ cos \ theta \ sin \ theta \ end { pmatrix} d \ theta \ propto \ int_0 ^ {\ pi / 2} \ begin {pmatrix} \ cos 2 \ theta + 1 \\ \ sin 2 \ theta \ end {pmatrix} d \ theta \ propto \ left [\ begin {pmatrix} \ sin 2 \ theta + 2 \ theta \\ - \ cos 2 \ theta \ end {pmatrix} \ right] _0 ^ {\ pi / 2} \ propto \ begin {pmatrix} \ pi \\ 2 \ end {pmatrix} $$

Cette impulsion nette a alors un angle par rapport à l'horizontale de $ \ arctan 2 / \ pi = 32,48 ° $ .

Par conservation d'énergie (puisque la collision est idéale) la balle doit sortir avec une vitesse égale à sa vitesse d'entrée, donc par addition parallélogramme de vecteurs l'angle par rapport à l'horizontale du changement de vitesse est la moitié de celui de la vitesse de sortie , donc l'angle de sortie doit être $ 2 \ arctan 2 / \ pi = 64,96 ° $ à l'horizontale.

Cela peut être répondu en considérant les cas extrêmes

• La balle est toujours en contact avec le sol en un seul point avec une réaction normale du mur agissant dans la direction opposée à celle de la balle.Ce cas se présenterait (au moment de frapper le mur) I lorsque le rayon de courbure y est inférieur à celui de la balle.

• La balle est toujours en contact avec la surface et a un point de contact unique avec la réaction normale toujours perpendiculaire à celle de la direction du mouvement.Ce cas se présenterait (au moment de frapper le mur) I lorsque le rayon de courbure y est supérieur à celui de la balle.

Maintenant, le cas que vous avez spécifié est un cas intermédiaire où la réaction normale agit dans la direction perpendiculaire ainsi que dans la direction opposée au mouvement, la balle s'envolerait du mur à un angle de 45 ° $ de l'horizontale.

Ok, voici ma supposition après une bonne quarante secondes de réflexion.Je pense qu'il rebondira du coin à un angle qui dépendra de sa vitesse.Le raisonnement est le suivant.Supposons des conditions parfaites, par exemple un frottement nul, une courbure parfaite, une élasticité parfaite, etc. Dans ce cas, l'impact sera instantané en tous points le long du quadrant inférieur droit de la balle.L'ampleur de la réaction à chaque point aura deux composantes, l'une due à l'effet de la gravité, l'autre due à l'impulsion de la collision.La composante gravitationnelle sera indépendante de la vitesse de la balle, l'autre composante augmentera avec la vitesse.Si l'on suppose que la vitesse est telle que la composante gravitationnelle peut être ignorée, alors en l'absence de frottement, la réaction doit partout être normale à la surface de contact, c'est-à-dire vers le centre de la balle.La somme des forces doit donc avoir une composante vers le haut et une composante vers la gauche, de sorte que la balle recule sous un certain angle.

Pour obtenir une réponse, il faut regarder la distribution normale de contactforce au moment de l'impact. Il devrait être évident que la force de contact sera la plus élevée à la hauteur de r sur le mur et de 0 au point de contact inférieur. Entre ces deux points, la force dépend de l'angle entre la vitesse et le vecteur normal. Comme je n'ai aucune information sur l'amplitude de la force, je la négligerai. L'angle résultant si $ \ alpha = 0 $ est où la force est $ 0 $ et $ \ alpha = \ pi / 2 $ où la force a son maximum peut être calculé par $ \ beta = \ frac {\ int_0 ^ {\ pi / 2} sin (\ alpha) \ alpha d \ alpha} {\ int_0 ^ {\ pi / 2} sin (\ alpha) d \ alpha} = 1 ~ rad = 57,3 ^ {\ circ} $ . Fondamentalement, la balle rebondira et reviendra dans la direction d'où elle vient avec un angle de $ \ gamma = 90 ^ {\ circ} -57,3 ^ {\ circ} = 32,7 ^ {\ circ} $ depuis le sol.

Edit: Dans cette image, la distribution de force normale est montrée et le vecteur de force résultant à l'impact est également montré. L'angle par rapport au sol est 32,7 $ ^ {\ circ} $ . Le noir représente les forces de contact normales et le rouge la force résultante.

La gravitation n'est pas incluse dans ce calcul car il n'y a aucune information sur la vitesse et le poids de la balle. Mais on pourrait donc faire le même calcul et changer les hypothèses pour que la force maximale à partir de la gravité soit au maximum à $ \ alpha = 0 $ et doit être $ 0 $ à $ \ alpha = \ pi / 2 $ . Par conséquent, le vecteur de force résultant de la force de contact gravitationnelle doit être à $ \ gamma = 57.3 ^ {\ circ} $ .

Edit2: j'ai oublié de prendre en compte que la gravité agit dans une direction différente puis l'autre force. La superposition doit en tenir compte.

Edit3: Correction de quelques fautes d'orthographe et ajusté la formule ci-dessus pour que la réponse ait les unités correctes.La formule elle-même provient du calcul du point d'attaque pour une charge linéaire ou une charge répartie.Il suffit de regarder l'angle comme une "coordonnée normale".J'ai également fait quelques calculs numériques et le résultat est donné comme $ 32.52 ^ {\ circ} $

Je pense que la réponse est assez simple.La balle se lèvera et se lèvera jusqu'à ce que toute son énergie cinétique ait été convertie en énergie potentielle.Si on essaie de visualiser, si le rayon de courbure du coin en collision est inférieur au rayon de la balle, il va évidemment entrer en collision avant de pouvoir se relever (bien qu'il puisse rebondir en raison d'une légère déformation en collision).Sinon, il peut augmenter.Cela devrait suffire :)